We can make an equation. How to write a chemical equation: rules, examples. Recording a chemical reaction. Compilation of binary formulas by valence

SECTION VI.

EQUALITY TRANSFORMATIONS.

___________

SOLUTION AND COMPILATION OF EQUATIONS OF THE 1ST DEGREE

§ 5. Compilation of an equation with one unknown.

Any arithmetic problem consists in the fact that according to several known quantities and according to given relationships between these known quantities and others, unknown ones, unknown ones are found. Algebra provides a special way to solve arithmetic problems. This method is based on the fact that the verbally expressed conditions of arithmetic problems can be translated into algebraic language, i.e. are expressible by means of algebraic formulas.

The translation of verbally expressed conditions of the problem into algebraic language is generally called formulating.

To compose an equation with one unknown according to the conditions of the problem means to translate these conditions into algebraic language in such a way that the entire set of these conditions is expressed by one equation containing one unknown. For this, it is necessary that the number of separate independent conditions of the problem be equal to the number of unknowns implied in it.

Due to the extreme diversity of problems, the methods for compiling equations corresponding to these problems are extremely diverse. General rules for compiling equations no. But there is one general indication that guides our reasoning when translating the conditions of the problem into algebraic language and allows us from the very beginning of the reasoning to follow the right path to achieve the final goal. This general indication, or the general principle of composing the equation, we will express as follows:

To compose an equation with one unknown according to the conditions of the problem, you need:

1) choose between the unknowns, which are either directly indicated in the problem, or implied, some one taken as the first, and designate this unknown with some letter, for example, X ;

2) using this designation and the designations given in the problem, express all the quantities that are directly mentioned in the problem or that are implied, observing that when compiling such expressions, all the numbers given in the problem and everything related to dains or to unknown values ​​of the condition;

3) after such an application of all the conditions, find between the composed or simply written expressions two such expressions that, by virtue of one of the given conditions, must be equal to each other, and connect these expressions with an equal sign.

Let's apply this principle to the solution of two problems:

Task 1 i. The number of coins in one wallet is half that in the other. If you lay out six coins from the first, and add eight coins to the second, then the number of coins in the first will be seven times less than in the second. Find out how many coins are in each wallet?

In this problem, several known and several unknown quantities are indicated. Let's take the first unknown number of coins of the first purse as the first unknown number and denote it by X. Then we will deal with the designation of all quantities, which include the conditions of the problem.

The number of coins in the first wallet is X . The ratio of the numbers of coins in the second and first wallets 2 . So the number of coins of the second wallet 2X.

Take out from the first 6 coins Therefore, in the first wallet there are coins X -6 .

In the second add 8 coins. Therefore, in the second wallet you will get coins 2X +8 . The new ratio between the numbers of coins of the second and first purse is . It is also equal 7 . On this basis, we compose an equation , solving which, we get x= 10 , after which it is not difficult to determine the other unknowns that we mentioned here.

If we took the second purse as the first unknown number of coins and denoted it to distinguish it from the previous designation through at , then, as is easy to see, another equation would be obtained, namely ( at + 8 ):( at / 2 -6 )=7 , which also solves the problem and gives the answer at=20 .

One could take for the first unknown the number of coins that appeared in the first purse after the calculation from it 6 coins; then, denoting this unknown by z and going in the same way as we went in the first equation, we would get the equation , where z = 4 .

But one could also change the very way in which the equation is correlated, for example, by taking into account the changed ratio between the numbers of coins, and basing the formulation of the equation on what is known about the original ratio. In this case, the equation would be written as follows:

The number of coins of the first wallet after the calculation is z . Posted 6 coins. So the initial number of coins of the first wallet z+ 6. Changed ratio between numbers of coins 7 . Therefore, the changed number of coins of the second wallet 7z. was added 8 coins. Therefore, the initial number of coins of the second purse 7z. - 8 . The initial ratio between the numbers of coins is It is equal to 2 . On this basis, we have an equation that is compatible with the previous one, although it differs from it in form.

If, going this second way, we took for the first unknown number of coins of the second purse after adding to it 8 coins, then, denoting this unknown for difference through and , we would get the equation ( and -8 ):( and / 7 + 6 )=2 , where and =28 .

These clarifications show that, guided by the same general rule for writing equations, we still get in each problem a variety of ways to achieve this goal. the best way the one that expresses the conditions of the problem more simply and leads faster both to the compilation and to the solution of the equation is considered. In this case, the first and third methods are equally convenient for solving the equation, but the first is still simpler and therefore better than the others.

In applying the above rule of formulating equations, it must be remembered that in any correctly expressed equation, every given number and every expressed condition must be taken into account.

Task 2. From the city BUT a traveler comes out, passing in the day along 20 verst. Two days later, she leaves the city to meet him. AT another traveler who passes daily by 30 verst. The distance between BUT and AT equals 190 verst. The question is, when and where will the two travelers meet?

1st way. Let us take as the first unknown time of movement of the first traveler from the exit from BUT before the meeting, and for the last condition is that the distance between BUT and AT equals 190 verst. Then we will argue like this:

Let's assume that the first one went before the meeting X days. Every day he walked 20 verst. So he went through 20X verst.

The second one came out later 2 day. So he went to meet X -2 day. Every day he walked 30 verst. Therefore, he went through 30 (X -2 ) verst. Together both travelers passed [ 20X + 30 (X -2 )] verst. All distance between BUT and AT equals 190 verst. Based on this, we find the equation

20X + 30 (X -2 ) =190 ,

where x= 5 . From this we see that the first traveler went 5 days and passed 100 verst, the second was 3 days and gone 90 verst.

2nd way. Let us take as the first unknown distance traveled by the first traveler from the exit to the meeting, and for the last condition that the second traveler left later than the first at 2 day. Then the discussion goes like this:

We believe that the first passed before the meeting at verst. Every day he walked 20 verst. So he walked all at / 20 days.

The second passed all ( 190 -at ) verst. Every day he walked 30 verst. So he walked only days.

The difference between the times of motion of both is and is equal to 2 . Therefore, we find the equation , where at =100 .

3rd way. The first unknown is the time of movement of the second traveler from the exit from AT see you, the last condition is that the first traveler passes daily 20 verst.

Let's assume that the second one goes to the meeting z days. So the first one will pass z +2 ) of the day. Walking daily through 30 verst, the second will pass only 30z verst. Since both need to pass 190 miles, then the first will have to do ( 190 -30z ) verst. To do this, he must do a mile a day. Since this expression is 20 , then the equation is obtained, whence z = 3.

4th way. The first unknown is the distance traveled by the second traveler before meeting, the last condition is that the second travels daily 10 versts more than the first.

We believe that the second passed before the meeting and verst. So the first one still had to go ( 190 -and ) verst. Since before the release of the second it has already passed 40 miles, then after the exit of the second he still had to go ( 150 -and ) verst. The difference in distances traveled simultaneously by both is ( 2and-150 ) verst. The time of their common movement is and / 30 days. Therefore, the second day passes more than the first by ( 2and-150 ) : and / 30 verst. Since this expression is 10 , then you get the equation ( 2and-150 ) : and / 30 =10 , which gives and = 90 .

The previous explanations show that the variety of ways to compose equations in the same problem depends both on the order of successively denoted quantities and on the order of successively taken into account conditions.

231. Two persons have together 38 rubles, and the first has 6 rubles more money than the second. How much money does each have?

231. Two persons have together 114 rubles, and the first has 18 rubles more money than the second. How much money does each have?

232. In one house, there are 15 fewer windows than in the other; in total, there are 51 windows in both houses. How many windows are in each?

232. In one house there are 6 less windows than in another; in total, both houses have 62 windows. How many windows are in each?

233. There are 81 rubles in two wallets. In the first, there is half as much money as in the second. How much money is in each?

233. There are 72 rubles in two wallets. In the first, there is five times less money than in the second. How much money is in each?

234. The father is three times older than the son, and the sum of the years of both of them is 48 years. Determine the age of both.

234. The father is twice as old as the son, and the sum of both years is 13 years. Determine the age of both.

235. The son is four times younger than the father, and the difference between their years is 27 years. How much to fly each?

235. The son is five times younger than the father, and the difference between their years is 32 years. How old is each?

236. There are 47 apples in three baskets, and the first and second baskets are equally divided, and the third has 2 more apples than each of the others. How many apples are in each basket?

236. There are 110 apples in three baskets, and the first and third are equally divided, and the second has 4 less apples than each of the others. How many apples are in each basket?

237. The three pieces of silver weigh together 48 pounds. The first is 12 pounds heavier than the second, and the third is 9 pounds heavier than the first. How much does each piece weigh?

237. Three pieces of silver weigh together 33 pounds. The first is 5 pounds lighter than the second, and the third is 2 pounds lighter than the first. How much does each piece weigh?

238. The son is 20 years younger than the father and 5 years older than the daughter. The sum of all three years is 60 years. How old is each

238. Mother is 21 years older than her son and 7 years younger than his father. The sum of all three years is 64 years. How old is each?

239. There are a total of 66 books on three shelves, with three times as many on the bottom and twice as many on the middle as on the top. How many books are on each shelf?

239. There are only 60 books on three shelves, and on the bottom there are six times more, and on the top five times more than on the middle one. How many books are on each shelf?

240. The forest, the garden and the meadow together cost 10,800 rubles. The meadow is 2 times more expensive than the garden, and the forest is 3 times more expensive than the meadow. What does each of them cost separately?

240. A forest, a garden and a meadow cost together 17,600 rubles. A forest is 3 times more expensive than a garden, and a meadow is 4 times more expensive than a forest. What does each of them cost separately?

241. Divide the number 21 into two parts so that the multiple of the ratio of the first part to the second is equal to the fraction 3/4.

241. Divide the number 48 into two parts so that the multiple ratio of the second part to the first is equal to the fraction 5/3.

242. Divide the number 88 into two parts so that the quotients of dividing the first part by 5 and the second by 6 are equal.

242. Divide the number 55 into two parts so that the quotients of dividing the first part by 7, a. the second by 4 were equal.

243. The sum of two numbers is 85 and their difference is 15. Find both numbers.

243. The sum of two numbers is 72, and their difference is 8. Find both numbers.

244. The difference of two numbers is 8, and their multiple ratio is equal to the fraction 3 / 2. Find these numbers.

244. The difference of two numbers is 12, and their multiple ratio is equal to the fraction 5/3. Find these numbers.

245. Divide the number 46 into two parts so that the difference of the quotients from dividing the first part by 3 and the second by 7 is equal to 2.

245. Divide the number 59 into two parts so that the difference of the quotients from dividing the first part by 3 and the second by 5 is equal to 1.

246. Divide the number 75 into two parts so that the larger part is three times the difference between the two parts.

246. Divide the number 56 into two parts so that the smaller part is three times the difference between the two parts.

247. The sum of two numbers is 64. When dividing a larger number by a smaller one, the quotient is 3 and the remainder is 4. Find these numbers.

247. The sum of two numbers is 45. When a larger number is divided by a smaller one, the quotient is 5 and the remainder is 3. Find these numbers.

248. The difference of two numbers is 35. When dividing a larger number by a smaller one, the quotient is 4 and the remainder is 2. Find these numbers.

248. Difference of two numbers 23. When dividing a larger number by a smaller one, the quotient is 2 and the remainder is 11. Find these numbers.

249. One of the two unknown numbers is greater than the other by 5. If you divide the smaller number by 4 and the larger number by 3, then the first quotient will be 4 less than the second. Find both numbers.

249. One of the two unknown numbers is greater than the other by 15. If you divide the larger number by 9 and the smaller by 2, then the first quotient will be 3 less than the second. Find both numbers.

250. One of the two unknown numbers is less than the other by 6. If you divide the larger number in half, then the resulting quotient will be three units less than the other number. Find both numbers.

250. One of the two unknown numbers is less than the other by 18. If you divide the larger number by three, then the resulting quotient will be two units greater than the other number. Find both numbers.

251. One tank has twice as much water as the other; if you pour 16 buckets from the first into the second, then there will be equal amounts of water in both. How much water is in each?

251. There is three times more water in one reservoir than in another; if you pour 22 buckets from the first into the second, then both will contain equal amounts of water. How much water is in each?

252. In the market, two traders have only 220 eggs; if the second of them gave the first 14 eggs, then the number of eggs for each of them would be the same. How many eggs does each have?

252. In the market, two traders have only 186 eggs; if the second of them gave the first 10 eggs, then the number of eggs for each of them would be the same. How many eggs does each have?

253. Someone has 4 times more rubles in his right pocket than in his left; if he transfers 6 rubles from his right pocket to his left, then there will be only 3 times more money in the right than in the left. How much money is in each pocket?

253. Someone has 3 times more rubles in his right pocket than in his left; if, however, 5 rubles are transferred from the left pocket to the right, then the right will contain five times more money than the left. How much money is in each pocket?

254. When two workers were paid at the factory, the first of them received 12 rubles more than the second for work, and after that the second worker paid him 2 rubles. debt. It turned out that the first brought home three times more money than the second. How much did each earn?

254. When calculating two workers at the factory, the first of them received 20 rubles less than the second for work, but at the same time the second worker returned 2 rubles to him. debt. It turned out that the first took home half the money of the second. How much did each earn?

255. One boy has 30 kopecks, the other 11 kopecks. How many times should they give one kopeck each so that the first has twice as much money as the second?

255. One boy has 48 kopecks, another has 22 kopecks. How many times do they have to spend one kopeck each so that the first has three times more money than the second?

256. The father is 40 years old and the son is 12 years old. How many years ago was the father five times older than the son?

256. The father is 49 years old and the son is 11 years old. In how many years will the father be three times as old as the son?

257. One landowner has four times as many sheep as another. If both bought 9 sheep each, then the first would have three times more sheep than the second. How many sheep does each have?

257. One landowner has three times less sheep than another. If both sold 10 sheep each, then the first would have five times fewer sheep than the second. How many sheep does each have?

258. The father is 39 years older than his son, and in 7 years he will be 4 times older than his son. How old is the one and the other?

258. Father and son together are 88 years old, and 8 years ago the father was 7 times older than his son. How old is the one and the other?

259. One tank has 48 buckets and the other has 22 buckets of water. Twice as much water was drained from the first as from the second, and then three times more water remained in the first than in the second. How many buckets are poured out of each?

259. There are 42 buckets in one tank and 8 buckets of water in another. Three times more water was poured into the first than into the second, and then four times more water turned out to be in the first than in the second. How many buckets are poured into each?

260. Two persons, playing cards separately, had at the beginning of the game - the first 72 rubles, the second 21 rubles. The first lost three times as much as the second won. After the game, the first player had twice as much money as the second player. How much did the second win and lose the first?

260. Two persons, playing cards separately, had at the beginning of the game - the first 25 rubles, the second 12 rubles. The first won twice as much as the second lost. After the game, the first player turned out to have five times more money than the second. How much did the second lose and the first win?

261. The peddler sold for the first time a part of 2/7 of the number of apples he had, for the second time p of the same number; then he had only 8 apples left. How many apples did he have?

261. The pedlar sold the first time 1/9 of the number of apples he had, the second time 5/6 of the same number; then he had only 4 apples left. How many apples did he have?

262. First, a third of the total amount of water was poured out of the water tank, then 5/6 of the rest, and then only 6 buckets remained. How much water was in the tank?

262. First, 3/5 of the total amount was poured out of the water tank, then 3/4 of the rest, and then only 5 buckets remained. How much water was in the tank?

263. In one society there were 40 men, women and children. The number of women was 3/5 of the number of men, and the number of children was 2/3 of the number of men and women together. How many men, women and children were there?

263. In one society there were 72 men, women and children. The number of men was 2/3 of the number of women, and the number of children was 4/5 of the number of men and women together. How many men, women and children were there?

264. For 30 arshins of cloth of two varieties, only 128 rubles were paid; a yardstick of the first grade costs 4 1/2 rubles, and a yardstick of the second grade costs 4 rubles. How many arshins of both grades were bought?

264. Only 120 rubles were paid for 27 arshins of cloth of two grades; arshin of the first grade costs 5 rubles; arshin of the second 3 p. 75 k.. How many arshins of both certificates were bought?

265. The tea merchant sold 38 pounds of tea of ​​two varieties, at a price of 3 r. per pound of the first grade and 1 p. 60 kopecks per pound of the second grade, and at the same time earned 22 rubles more for the entire first grade than for the second. How many teas of both varieties were sold?

265. A tea merchant sold 110 pounds of tea of ​​two varieties, at a price of 4 1/2 r. per pound of the first grade and 2 p. 25 k. for a pound of the second grade, and at the same time gained 45 rubles less for the first grade than for the second. How many teas of both varieties were sold?

266. The contractor hired an employee on the condition of paying him 90 kopecks. for each working day and deduct 40 kopecks from it. for each non-working day. After 12 days, the worker received 6 r. 90 k.. How many days did he work?

266. The contractor hired an employee on the condition of paying him 80 kopecks. for each working day and deduct 50 kopecks from it. for each non-working day. After 50 days, the worker received 21 rubles. 80 in .. How many days did he skip?

267. BUT and AT they play billiards with the condition that the winner of the game receives 76 k from the loser; after 20 games it turned out that AT won only 4 r. 50 k.. How many games did he win?

267 BUT and AT they play billiards with the condition that the winner of the game receives 50 k from the loser; after 12 games it turned out that BUT won only 2 times. How many games did he lose?

268. Two couriers left at the same time from two cities located at a distance of 300 miles, and are traveling towards one another. The first travels 12 versts per hour, the second 13 versts. When will they meet?

268. Two couriers left at the same time from two cities located at a distance of 280 miles, and go towards one another. The first travels 11 versts per hour, the second 17 versts. When will they meet?

269. from two stations railway, located at a distance of 77 versts, two trains leave at the same time and go in the same direction at speeds of 31 1/2 versts and 18 2/3 versts per hour, with the first following the second. When will he catch up?

269. From two railway stations located at a distance of 38 versts, two trains leave simultaneously and go in the same direction at speeds of 25 1/4 versts and 20 1/2 versts per hour, the first following the second. When will he catch up?

270. A passenger train leaves the station at 12 noon, making 32 in. at one o'clock. After 45 minutes, a courier train leaves the same station, making 42 in. at one o'clock. At what time will the courier train overtake the passenger train?

270. A passenger train leaves the station at 9 o'clock in the morning, making 28 in. at one o'clock. An hour and a quarter later, a courier train leaves the same station, making 40 volts. at one o'clock. At what time will the courier train overtake the passenger train?

271. What capital needs to be given in growth at 6% in order to make a profit of 224 rubles in 1 year 2 months?

271. What capital must be given up for growth at 8% in order to receive a profit of 182 rubles in 7 months?

272. How much interest must be given to capital growth of 4400 rubles in order to receive a profit of 280 rubles in 1 year 5 months. 50 k.?

272. How much interest must be given in growth of a capital of 1800 rubles in order to receive a profit of 93 rubles in 11 months. 60 k.?

273. The merchant, having sold the goods for 299 rubles, gained 15% of the profit. What does the product cost him?

273. A merchant, having sold goods for 161 rubles, received 7 1/2% of the profit. What does the product cost him?

274. When selling goods in the amount of 429 p. received at a loss of 2 1/2%. What is the price of a product?

274. When selling goods in the amount of 366 rubles. received at a loss 8 1 / 2 % What is the cost of the goods?

275. On the bill 10 months before the due date, 1120 rubles were paid, with commercial accounting at 8%. Find the currency of the bill.

275. On a bill for 1 year 3 months before the due date, 839 rubles were paid. 60 kop. with commercial accounting at 7%. Find the currency of the bill.

276. The pool fills with one pipe at 3 o'clock, the other at 5 o'clock. How long will it take to fill up if both pipes are opened at the same time?

276. The pool is filled with one pipe at 7 1/2 o'clock, the other at 5 o'clock. How long will it take to fill up if both pipes are opened at the same time?

277. The pool is filled with one pipe at 4 o'clock, and through the other it can all flow out at 6 o'clock. At what time will the pool be filled with the simultaneous action of both pipes?

277. The pool is filled with one pipe at 2 1 / 3 hours, and through the other it can all flow out at 2 hours 48 hours. How long will the pool be filled with the simultaneous action of both pipes?

278. Two workers together finish work at 3 hours 36 minutes; the first one can perform it at 6 o'clock. At what time will the second person do the same work?

278. Two workers together finish work at 12 o'clock; the first one can perform it at 20 o'clock. At what time will the second one do the same work?

279. There are three pipes in the pool; water enters through the first two, flows out through the third. Through the first pipe, the pool can be filled at 3 o'clock, through the second at 2 o'clock, and through the third all the water can flow out of the pool at 6 o'clock. At what time will the pool be filled if all three pipes are opened?

279. There are three pipes in the basin; water enters through the first two, flows out through the third. Through the first pipe, the pool can be filled at 2 o'clock, through the second at 5 o'clock, and through the third, all the water can flow out of the pool at 10 o'clock. At what time will the pool be filled if all three pipes are opened?

280. Of the three pipes drawn into the pool, the first fills it at 5 o'clock, the second fills it at 15 o'clock, and through the third the entire pool flows out at 3 o'clock. How long will it take for a full pool to drain if all pipes are active at the same time?

280. Of the three pipes drawn into the pool, the first fills it at 6 o'clock, the second fills it at 18 o'clock, and through the third the entire pool flows out at 3 o'clock. How long will it take for the full pool to drain if all the pipes operate simultaneously?

281. The second train of the railway goes from BUT in AT at an average speed of 30 miles per hour, then returns from AT in BUT at a speed of 28 miles per hour. He makes the whole trip there and back at 2 1/2 hours. How many miles from BUT before AT?

281. The second train of the railway goes from BUT in AT at an average speed of 24 miles per hour, then returns from AT in BUT at a speed of 30 miles per hour. He makes the whole trip there and back at 11 1/4 hours. How many miles from BUT before AT?

282. From BUT in AT a train came out, passing at an hour of 20 versts. After 8 hours the train leaves AT in BUT, passing 30 in. at one o'clock. Distance AB equals 350 V.. At what distance from BUT trains meet?

282. From BUT in AT a train came out, passing at the hour of 24 versts. The train leaves in 5 hours. AT in BUT passing 28 c. at one o'clock. Distance AB equal to 380 in., At what distance from AT trains meet?

283. The sum of three numbers is 70. The second number, when divided by the first, gives a quotient of 2 and a remainder of 1, the third, when divided by the second, gives a quotient of 3 and a remainder of 3. Find these numbers.

283. The sum of three numbers is 60. The second number, when divided by the first, gives a quotient of 3 and a remainder of 2; the third, when divided by the second, gives a quotient of 2 and a remainder of 4. Find the numbers.

284. Find a number which, when divided by 5, leaves a remainder of 2, and when divided by 8, gives a remainder of 5, knowing that the first quotient is three times greater than the second.

284. Find a number which, when divided by 7, leaves a remainder of 2, and when divided by 9, gives a remainder of 4, knowing moreover. that the first quotient is two greater than the second.

285. Someone, wanting to distribute the money he had with him to the poor, calculated that if each was given 15 kopecks, then 10 kopecks would not be enough for him, and if each were given 13 kopecks, then 6 kopecks would remain extra. How many beggars were there and how much money?

285. Someone, wishing to distribute the money he had with him to the poor, calculated that if everyone was given 8 kopecks, then 4 kopecks would remain. superfluous, and if everyone is given 9 kopecks, then 2 kopecks will not be enough .. How many beggars were there and how much money?

286. The engineer places telegraph poles at some distance. If he put them at a distance of 25 fathoms from one another, then 150 more pillars would have to be made, and if he increased the distance between the pillars by 5 fathoms, then 70 pillars would be extra. How great is the distance and how many poles are made?

286. An engineer places telegraph poles at some distance. If he put them at a distance of 30 fathoms from one another, then he would have 100 extra pillars left, and if he reduced the distance of the pillars by 4 fathoms, then another 180 pillars would have to be made. How great is the distance and how many poles are made?

287. Someone, when hiring a servant, promised him for a year of service to pay money and 144 rubles. and give clothes. The servant paid off after 7 months and received clothes and 54 rubles in payment. What did the clothes cost?

287. When hiring a servant, someone promised to pay him 75 rubles in money for 7 months of service and give him clothes. The servant paid off after 5 months and received clothes and 45 rubles in payment. What is the cost of clothes?

288. Paid for 46 pounds of sugar for 195 rubles. more than 73 pounds of tea; 9 poods of sugar cost 30 rubles less than 37 pounds of tea. What is a pound of tea and a pood of sugar worth?

288. Paid for 21 pounds of tea for 238 rubles less than for 40 pounds of sugar; 15 pounds of tea cost 2 rubles. more expensive than 4 poods of sugar. What is a pound of tea and a pood of sugar worth?

289. The landowner hired two peasants for the same daily wage. One of them for 40 days, he gave 7 p. 50 kopecks in money and 3 1/2 quarters of oats, another 4 rubles in 24 days. 80 k. in cash and 2 quarters of oats. What is a quarter of an oat worth?

289. The landowner hired two peasants for the same daily wage. He gave 14 rubles to one of them in 56 days. money and 8 quarters of oats, another for 88 days 13 p. 50 k. in cash and 15 quarters of oats. What is the cost of a quarter of an oat?

290. Paid for 25 arshins of cloth and 21 arshins. velvet 247 rubles. It is known that 10 arsh. velvet cost 18 rubles more than 13 arshins of cloth. What is worth an arshin of both?

290. Paid for 15 arshins of velvet and 52 arshins. cloth 276 rubles. It is known that 2 arsh. velvet cost 17 rubles less than 11 arsh. cloth. What is worth an arshin of both?

291. The sum of the digits of a two-digit number is 12. If 18 is subtracted from the desired number, then you get a number indicated by the same digits, but written in reverse order. Find this number.

291. The difference between the digits of units and tens of some two-digit number is equal to 3. If 27 is added to the desired number, then we get a number indicated by the same digits, but written in reverse order. Find this number.

292. In some two-digit number, the number of tens is twice the number of units. If we rearrange the digits of this number, then we get a number less than the desired one by 36. Find this number.

292. In some two-digit number, the number of tens is three times less than the number of units. If we rearrange the digits of this number, we get a number greater than the desired one by 36. Find this number.

293. A playing chess with AT and wins three out of every four games against him, then plays with With and wins two out of every three games against the latter. Total BUT played 21 games and won 15 of them. How many games did he play with AT and with With?

293. BUT playing chess with AT and loses to him three out of every eight games, then plays with With and loses two out of every five games to the last. Generally BUT played 26 games and lost 10 of them. How many games did he play with AT and with With?

294. What time is it now if 1/5 of the number of hours since noon is 1/3 of the number of hours until midnight?

294. What time is it now, if 1/11 of the number of hours that have passed since noon is equal to 1/13 of the number of hours left until midnight?

295. Find the weight of the fish, knowing that the tail weighs 2 pounds, the head weighs as much as the tail and half of the body, and the body weighs as much as the head and tail.

295. Find the weight of the fish, knowing that its head weighs 7 pounds, the tail weighs as much as the head and half of the body weigh, and the body weighs as much as the tail and head.

296. A certain amount must be divided by two persons so that the parts of the first and second are related to each other like the numbers 5 and 3, and that part of the first is 50 rubles. over 5/9 of the total. How big is each part?

296. A certain amount must be divided between two persons so that the parts of the first and second are related to each other as the numbers 7 and 4, and that the part of the second is 21 rubles. less than 5/12 of the whole sum. How big is each part?

297. The product was sold at a loss for 420 rubles; if it were sold for 570 rubles, then the profit received would be 5 times more than the loss incurred. What is the price of a product?

297. Goods sold at a profit for 520 rubles; if it had been sold for 320 rubles, then there would have been a loss amounting to 3/7 of the proceeds. What is the price of a product?

298. The numbers of arshins of calico contained in three pieces are related as 2:3:5. If you cut off 4 arshins from the first piece, 6 arshins from the second. and from the third 10 arsh., then the remaining amount of the whole chintz will be 5/6 of the previous amount. How many arshins are in each piece?

298. The number of arshins of calico contained in three pieces is 3:5:8. If cut off from the first 10 arshins, from the second 20 arshins. and from the third 30 arsh., then the remaining amount of the whole chintz will be 5/8 of the previous amount. How many arshins are in each piece?

299. First, half of all the water in it and half a bucket were poured out of the reservoir, then half of the remainder and half a bucket, finally another half of the remainder and half a bucket; after that, 6 buckets remained in the tank. How much water was there in the beginning?

299. A third of the water that was in it and a third of a bucket were poured out of the reservoir, then a third of the remainder and a third of the bucket, finally another third of the remainder and a third of the bucket; after that, 7 buckets remained in the tank. How much water was there at the beginning?

300. Several persons divide some amount as follows; the first one gets 100 r. and a fifth of the remainder, the second 200 rubles and a fifth of the new balance, the third 300 rubles and a fifth of the remainder, etc. It turned out that the entire amount was divided into equal parts. How big is this amount, how many participants are in the division and how much did each get?

300. Several persons divide a certain amount as follows: the first receives 50 rubles and a sixth of the balance, the second 100 rubles and a sixth of the new balance, the third 150 rubles and a sixth of the balance, etc. It turned out that the entire amount was divided into equal parts . How big is this amount, how many participants are in the division and how much did each get?

The following tasks differ from the previous ones in that the data is expressed implicitly, namely in letters. These tasks belong to the same types as the previous ones. When solving them, the most important of those methods that were used earlier are repeated, but, due to the implicit form of the data, the reasoning is more general and at the same time more abstract. In the new exercises, just as in the previous ones, one must first of all take care to express through the main unknown and through the given designations all the quantities that are directly mentioned in the problem or that are implied in it, and in this case one must consistently take into account attention to all the designations given in the problem, and all the conditions related to the data and to those sought, when in this way all the conditions will be used in the case, then the thought of how to compose the required equation will itself appear.

301. Difference of two numbers s q . Find both numbers.

301. Difference of two numbers d , the multiple ratio of the larger to the smaller q . Find both numbers.

302. Divide a number a into three parts so that the first part is greater than the second by a number t and less than a third P once.

302. Divide a number a into three parts so that the first part is less than the second by a number t and more than a third P once.

303. One number in a times less than the other. If you add to the first number t , and to the second P , then the first sum will be in b times less than the second. Find these numbers.

303. One number in a times less than the other. If we subtract from the first t , and from the second P , then the first difference will be in b times more than the second. Find these numbers.

304. The number of a fraction is less than its denominator by a number a ; If, however, the fractions are subtracted from both members by b t / P . Find terms of a fraction.

304. The numerator of a fraction is greater than its denominator by a number a . If we add to both members of the fraction by b , then you get a fraction equal to the fraction t / P . Find terms of a fraction.

305. Divide a number a R times more than the second and q times less than a third.

305. Divide a number a into three parts so that the first was. in R times less than the second and q times more than a third.

306. The denominator of a fraction is the largest of its numerator in a once. If we add to the numerator the number b and subtract the number from the denominator with , then you get a fraction equal to the fraction k /l . Find terms of a fraction.

306. The denominator of a fraction is less than its numerator in a once. If we subtract the number from the numerator b and add a number to the denominator with , then learn a fraction equal to the fraction k /l . Find terms of a fraction.

307. Divide a number t into two parts so that the difference between the quotients from dividing the first part by a and second on b would love r.

307. Divide a number t into two parts so that the sum of the quotients from dividing the first part by a and second on b would equal s .

308. An employee receives for each working day a kopecks, and for each non-working one they deduct b kopecks. After the lapse of P days, the net income of the worker is equal to s rubles. How many working days and how many non-working days?

308. An employee receives for each working day a kopecks, and for each non-working one they deduct from it b kopecks. After the lapse of P days, the employee must pay 5 rubles himself. How many working days and how many non-working days?

309. Difference of two numbers d . Dividing the minuend by the subtrahend gives the quotient q and a remainder equal to half the difference. Find those numbers

309. Difference of two numbers d . Dividing the minuend by the subtrahend gives the remainder r and a quotient equal to half the difference. Find these numbers.

310. For a few arshins of cloth. paid a rubles; if we bought more cloth with b

310. Paid for a few arshins of cloth a rubles; if we bought cloth for less with arshin, then you would have to pay b rubles. How many arshins were bought?

311. What number, when multiplied by a , will increase by the number t ?

311. What number, being divided by a , decrease by the number t ?

312. When selling a house for m rubles received R percent loss. What did it cost the seller himself?

312. When selling a house for t ruble received R percent profit. What did it cost the seller himself?

313. Two couriers leave at the same time from two places BUT and AT and travel in the same direction BUT to AT and so on. ІІfirst passes in an hour a verst, second b verst. Distance AB equals d verst. When and how far from BUT Will the first courier overtake the second?

313. Two couriers leave at the same time from two places BUT and AT and go towards one another. The first one passes in an hour a verst, second b verst. Distance AB equals d verst. When. and how far from BUT will both couriers meet?

314. The front wheel of the carriage has a circumference of a feet, rear circumference b ft. How far must the carriage travel in order for the front wheel to make P high revs in reverse?

314. The front wheel of the carriage has a circle on a feet less than the rear. How far must the carriage travel for the front wheel to make t , and the back P revolutions?

315. Two pipes are led into the pool, both of which fill it, the first with a separate action in a hours, the second also with a separate action in b hours. At what time will the pool be filled with the simultaneous action of both pipes?

315. Two pipes are led into the pool, of which the first, with a separate action, fills it in a hours, and the second also, in a separate action, pours the entire pool into b hours. How long will it take to fill the pool with simultaneous operation of both pipes?

316. Crew wheel circumference a times the circumference of the front wheel. The crew passed t feet, and in doing so, the front wheel made to revolutions more than the rear. Determine the circumference of both wheels and the number of revolutions.

316. The circumference of the front wheel on a feet less than the rear circumference. The crew passed t feet, and at the same time the rear wheel did in to times less revolutions than the front. Determine the circumference of both wheels and the number of revolutions.

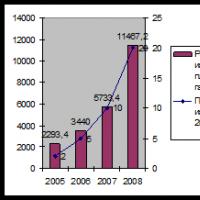
317. The population of one city increases annually by R % compared to the population of the previous year. Currently in the city t

317. The population of one city decreases annually by R % compared to the population of the previous year. Currently in the city t residents. How many people were there 3 years ago?

318. Two workers, working at the same time, finish their work in a hours. One first will do the same job in b , times faster than one second. At what time will each worker finish work?

318. Two workers, working at the same time, finish work in a hours. One first will do the same job in b , times slower than one second. What time does each worker finish work?

319. The boatman, rowing down the river, swims P sazhen in t hours; rowing against the current, he uses and more hours to swim the same distance. Determine the hourly flow rate.

319. A boatman, rowing against the current, swims P sazhen in t hours; paddling downstream, he uses and hours less to swim the same distance. Determine the hourly flow rate.

320. body BUT moving at a speed v meters per second. How fast should the other body move? AT, coming from the same place t seconds earlier if it was overtaken by the body BUT through and seconds after the start of the movement of this body?

320. Body A moving at a speed v meters per second. How fast should the other body move? AT coming from the same place and seconds later if it catches up with the body BUT through and seconds after the start of its movement?

321. Of the two varieties of goods, at a price of a rubles and b rubles per pound, compiled d t rubles per pound received s rubles loss. How many pounds of both sorts went into making the mixture?

321. Of two varieties of goods, at a price of a rubles and b rubles per pound, compiled d pounds of mix. When selling this mixture by t rubles per pound received s rubles profit. How many pounds of both sorts went into making the mixture?

322. B pool, accommodating t buckets, two pipes were laid. The first pours into the pool a buckets per hour. The second pours the entire pool into b hours. At what time will the pool be filled with simultaneous operation of both pipes?

322. To the pool containing t buckets, two pipes were laid. The first fills the entire pool in a hours. The second in an hour pours out of the pool b buckets. At what time will the pool be filled with simultaneous operation of both pipes?

323. Divide a number a into three parts so that the first relates to the second, as t:p , and the second to the third, as p: q.

323. Divide a number a into three parts so that the second relates to the first, as t:p , and the third to the second, as p: q.

324. From two places BUT and AT P sazhen, two boats are sailing towards each other, driven by rowers with the same strength. The first, floating downstream, travels the entire distance AB in t hours; the second, swimming against the current, uses the same distance more time for and hours. Determine the hourly flow rate.

324. From two places BUT and AT on the river, separated from one another by P sazhen, two boats are sailing towards each other, driven by rowers with the same strength. The first, swimming against the current, travels the entire distance AB in t hours; the second, going with the flow, consumes less time for the same distance and hours. Determine the hourly flow rate.

325. Determine the capitals of three persons, knowing that the first and the second have together t rubles, the second with the third P rubles, and that the capital of the first R times less than the capital of the third.

325. Determine the capitals of three persons, knowing that the first and the third have together t rubles, the second with the third P rubles, and that the capital of the first R times the capital of the second.

326. Two bodies move towards each other from two places at a distance d meters. The first moves at a speed v meters per second. With what speed should the second body move if it has reached the h seconds later than the first and should go before the meeting of everything P seconds?

326. Two bodies move towards one another from two places at a distance d meters. The first moves at a speed v meters per second. With what speed must the second body move if it has reached h seconds before the first and should go until the meeting of all P seconds?

327. Promissory note discounted commercially R % behind P years before the deadline, gives more mathematical consideration, also made according to R % and for P years, on a rubles. Find the currency of the week.

327. A bill discounted commercially R % behind P years, stands on t rubles cheaper than with mathematical accounting, also made according to R % and for P years What is the amount of the bill?

328. Two couriers leave places BUT and B located at a distance d verst, and they go towards, passing at the first hour u version and second v versts; departure of the first BUT took place on h AT. Determine when and where the couriers will meet?

328. Two couriers leave places BUT and B located at a distance d verst, and they both go in the same direction, passing at an hour or one and verst and second v versts; departure first from BUT took place on h hours before the departure of the second B. Determine when and where the first courier will overtake the second?

329. Divide a number a into such three parts, that if you attach to the first t , the second is first reduced by m , and then multiply by P , and divide the third into P , then the results will be the same.

329. Divide a number a into such three parts that if the first is reduced by t , first increase the second by t , then multiply by P , and divide the third into P , then the results will be the same.

330. There are three pipes in the pool. A, B and With. Through BUT and With water flows through AT BUT and AT the pool fills up t hours, under action BUT and C in P hours, under action AT and With in R hours. At what time will the pool be filled with the simultaneous action of all three pipes?

330. Three pipes are led into the pool A, B and With. Through BUT water flows through AT and With follows. With the joint action of pipes BUT and AT the pool fills up t hours, under action BUT and With in P clock, pipes AT and With pour the whole pool into R hours. How long will it take for the entire pool to drain if all three pipes operate simultaneously?

This article continues the theme of the equation of a straight line on a plane: consider this type of equation, as general equation straight. Let's define a theorem and give its proof; Let's figure out what an incomplete general equation of a straight line is and how to make transitions from a general equation to other types of equations of a straight line. We will consolidate the whole theory with illustrations and solving practical problems.

Let a rectangular coordinate system O x y be given on the plane.

Theorem 1

Any equation of the first degree, having the form A x + B y + C \u003d 0, where A, B, C are some real numbers (A and B are not equal to zero at the same time) defines a straight line in a rectangular coordinate system on the plane. In turn, any line in a rectangular coordinate system on the plane is determined by an equation that has the form A x + B y + C = 0 for a certain set of values ​​A, B, C.

Proof

This theorem consists of two points, we will prove each of them.

1. Let us prove that the equation A x + B y + C = 0 defines a line on the plane.

Let there be some point M 0 (x 0 , y 0) whose coordinates correspond to the equation A x + B y + C = 0 . Thus: A x 0 + B y 0 + C = 0 . Subtract from the left and right sides of the equations A x + B y + C \u003d 0 the left and right sides of the equation A x 0 + B y 0 + C \u003d 0, we get a new equation that looks like A (x - x 0) + B (y - y 0) = 0 . It is equivalent to A x + B y + C = 0 .

The resulting equation A (x - x 0) + B (y - y 0) = 0 is a necessary and sufficient condition for the perpendicularity of the vectors n → = (A, B) and M 0 M → = (x - x 0, y - y 0 ) . Thus, the set of points M (x, y) defines in a rectangular coordinate system a straight line perpendicular to the direction of the vector n → = (A, B) . We can assume that this is not so, but then the vectors n → = (A, B) and M 0 M → = (x - x 0, y - y 0) would not be perpendicular, and the equality A (x - x 0 ) + B (y - y 0) = 0 would not be true.

Therefore, the equation A (x - x 0) + B (y - y 0) \u003d 0 defines some line in a rectangular coordinate system on the plane, and therefore the equivalent equation A x + B y + C \u003d 0 defines the same line. Thus we have proved the first part of the theorem.

1. Let us prove that any straight line in a rectangular coordinate system on a plane can be given by an equation of the first degree A x + B y + C = 0 .

Let's set a straight line a in a rectangular coordinate system on the plane; point M 0 (x 0 , y 0) through which this line passes, as well as the normal vector of this line n → = (A , B) .

Let there also exist some point M (x , y) - a floating point of the line. In this case, the vectors n → = (A , B) and M 0 M → = (x - x 0 , y - y 0) are perpendicular to each other, and their scalar product is zero:

n → , M 0 M → = A (x - x 0) + B (y - y 0) = 0

Let's rewrite the equation A x + B y - A x 0 - B y 0 = 0 , define C: C = - A x 0 - B y 0 and finally get the equation A x + B y + C = 0 .

So, we have proved the second part of the theorem, and we have proved the whole theorem as a whole.

Definition 1

An equation that looks like A x + B y + C = 0 - This general equation of a straight line on a plane in a rectangular coordinate systemO x y .

Based on the proved theorem, we can conclude that a straight line given on a plane in a fixed rectangular coordinate system and its general equation are inextricably linked. In other words, the original line corresponds to its general equation; the general equation of a straight line corresponds to a given straight line.

It also follows from the proof of the theorem that the coefficients A and B for the variables x and y are the coordinates of the normal vector of the straight line, which is given by the general equation of the straight line A x + B y + C = 0 .

Consider specific example general equation of a straight line.

Let the equation 2 x + 3 y - 2 = 0 be given, which corresponds to a straight line in a given rectangular coordinate system. The normal vector of this line is the vector n → = (2 , 3) ​​. Draw a given straight line in the drawing.

The following can also be argued: the straight line that we see in the drawing is determined by the general equation 2 x + 3 y - 2 = 0, since the coordinates of all points of a given straight line correspond to this equation.

We can get the equation λ · A x + λ · B y + λ · C = 0 by multiplying both sides of the general straight line equation by a non-zero number λ. The resulting equation is equivalent to the original general equation, therefore, it will describe the same line in the plane.

Definition 2

Complete general equation of a straight line- such a general equation of the line A x + B y + C \u003d 0, in which the numbers A, B, C are non-zero. Otherwise, the equation is incomplete.

Let us analyze all variations of the incomplete general equation of the straight line.

1. When A \u003d 0, B ≠ 0, C ≠ 0, the general equation becomes B y + C \u003d 0. Such an incomplete general equation defines a straight line in the rectangular coordinate system O x y that is parallel to the O x axis, since for any real value of x, the variable y will take on the value - C B . In other words, the general equation of the line A x + B y + C \u003d 0, when A \u003d 0, B ≠ 0, defines the locus of points (x, y) whose coordinates are equal to the same number - C B .
2. If A \u003d 0, B ≠ 0, C \u003d 0, the general equation becomes y \u003d 0. Such an incomplete equation defines the x-axis O x .
3. When A ≠ 0, B \u003d 0, C ≠ 0, we get an incomplete general equation A x + C \u003d 0, defining a straight line parallel to the y-axis.
4. Let A ≠ 0, B \u003d 0, C \u003d 0, then the incomplete general equation will take the form x \u003d 0, and this is the equation of the coordinate line O y.
5. Finally, when A ≠ 0, B ≠ 0, C \u003d 0, the incomplete general equation takes the form A x + B y \u003d 0. And this equation describes a straight line that passes through the origin. Indeed, the pair of numbers (0 , 0) corresponds to the equality A x + B y = 0 , since A · 0 + B · 0 = 0 .

Let us graphically illustrate all the above types of the incomplete general equation of a straight line.

Example 1

It is known that the given straight line is parallel to the y-axis and passes through the point 2 7 , - 11 . It is necessary to write down the general equation of a given straight line.

Decision

A straight line parallel to the y-axis is given by an equation of the form A x + C \u003d 0, in which A ≠ 0. The condition also specifies the coordinates of the point through which the line passes, and the coordinates of this point correspond to the conditions of the incomplete general equation A x + C = 0 , i.e. equality is correct:

A 2 7 + C = 0

It is possible to determine C from it by giving A some non-zero value, for example, A = 7 . In this case, we get: 7 2 7 + C \u003d 0 ⇔ C \u003d - 2. We know both coefficients A and C, substitute them into the equation A x + C = 0 and get the required equation of the line: 7 x - 2 = 0

Answer: 7 x - 2 = 0

Example 2

The drawing shows a straight line, it is necessary to write down its equation.

Decision

The given drawing allows us to easily take the initial data for solving the problem. We see in the drawing that the given line is parallel to the O x axis and passes through the point (0 , 3) ​​.

The straight line, which is parallel to the abscissa, is determined by the incomplete general equation B y + С = 0. Find the values ​​of B and C . The coordinates of the point (0, 3), since a given straight line passes through it, will satisfy the equation of the straight line B y + С = 0, then the equality is valid: В · 3 + С = 0. Let's set B to some value other than zero. Let's say B \u003d 1, in this case, from the equality B · 3 + C \u003d 0 we can find C: C \u003d - 3. Using the known values ​​of B and C, we obtain the required equation of the straight line: y - 3 = 0.

Answer: y - 3 = 0 .

General equation of a straight line passing through a given point of the plane

Let the given line pass through the point M 0 (x 0, y 0), then its coordinates correspond to the general equation of the line, i.e. the equality is true: A x 0 + B y 0 + C = 0 . Subtract the left and right sides of this equation from the left and right sides of the general complete equation straight. We get: A (x - x 0) + B (y - y 0) + C \u003d 0, this equation is equivalent to the original general one, passes through the point M 0 (x 0, y 0) and has a normal vector n → \u003d (A, B) .

The result that we have obtained makes it possible to write the general equation of a straight line with known coordinates of the normal vector of the straight line and the coordinates of a certain point of this straight line.

Example 3

Given a point M 0 (- 3, 4) through which the line passes, and the normal vector of this line n → = (1 , - 2) . It is necessary to write down the equation of a given straight line.

Decision

The initial conditions allow us to obtain the necessary data for compiling the equation: A \u003d 1, B \u003d - 2, x 0 \u003d - 3, y 0 \u003d 4. Then:

A (x - x 0) + B (y - y 0) = 0 ⇔ 1 (x - (- 3)) - 2 y (y - 4) = 0 ⇔ ⇔ x - 2 y + 22 = 0

The problem could have been solved differently. The general equation of a straight line has the form A x + B y + C = 0 . The given normal vector allows you to get the values ​​of the coefficients A and B , then:

A x + B y + C = 0 ⇔ 1 x - 2 y + C = 0 ⇔ x - 2 y + C = 0

Now let's find the value of C, using the point M 0 (- 3, 4) given by the condition of the problem, through which the line passes. The coordinates of this point correspond to the equation x - 2 · y + C = 0 , i.e. - 3 - 2 4 + C \u003d 0. Hence C = 11. The required straight line equation takes the form: x - 2 · y + 11 = 0 .

Answer: x - 2 y + 11 = 0 .

Example 4

Given a line 2 3 x - y - 1 2 = 0 and a point M 0 lying on this line. Only the abscissa of this point is known, and it is equal to - 3. It is necessary to determine the ordinate of the given point.

Decision

Let's set the designation of the coordinates of the point M 0 as x 0 and y 0 . The initial data indicates that x 0 \u003d - 3. Since the point belongs to a given line, then its coordinates correspond to the general equation of this line. Then the following equality will be true:

2 3 x 0 - y 0 - 1 2 = 0

Define y 0: 2 3 (- 3) - y 0 - 1 2 = 0 ⇔ - 5 2 - y 0 = 0 ⇔ y 0 = - 5 2

Answer: - 5 2

Transition from the general equation of a straight line to other types of equations of a straight line and vice versa

As we know, there are several types of the equation of the same straight line in the plane. The choice of the type of equation depends on the conditions of the problem; it is possible to choose the one that is more convenient for its solution. This is where the skill of converting an equation of one kind into an equation of another kind comes in very handy.

First, consider the transition from the general equation of the form A x + B y + C = 0 to the canonical equation x - x 1 a x = y - y 1 a y .

If A ≠ 0, then we transfer the term B y to the right side of the general equation. On the left side, we take A out of brackets. As a result, we get: A x + C A = - B y .

This equality can be written as a proportion: x + C A - B = y A .

If B ≠ 0, we leave only the term A x on the left side of the general equation, we transfer the others to the right side, we get: A x \u003d - B y - C. We take out - B out of brackets, then: A x \u003d - B y + C B.

Let's rewrite the equality as a proportion: x - B = y + C B A .

Of course, there is no need to memorize the resulting formulas. It is enough to know the algorithm of actions during the transition from the general equation to the canonical one.

Example 5

The general equation of the line 3 y - 4 = 0 is given. It needs to be converted to a canonical equation.

Decision

We write the original equation as 3 y - 4 = 0 . Next, we act according to the algorithm: the term 0 x remains on the left side; and on the right side we take out - 3 out of brackets; we get: 0 x = - 3 y - 4 3 .

Let's write the resulting equality as a proportion: x - 3 = y - 4 3 0 . Thus, we have obtained an equation of the canonical form.

Answer: x - 3 = y - 4 3 0.

To transform the general equation of a straight line into parametric ones, first, the transition to the canonical form is carried out, and then the transition from the canonical equation of the straight line to parametric equations.

Example 6

The straight line is given by the equation 2 x - 5 y - 1 = 0 . Write down the parametric equations of this line.

Decision

Let's make the transition from the general equation to the canonical one:

2 x - 5 y - 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Now let's take both parts of the resulting canonical equation equal to λ, then:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

Answer:x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

The general equation can be converted to a straight line equation with a slope y = k x + b, but only when B ≠ 0. For the transition on the left side, we leave the term B y , the rest are transferred to the right. We get: B y = - A x - C . Let's divide both parts of the resulting equality by B , which is different from zero: y = - A B x - C B .

Example 7

The general equation of a straight line is given: 2 x + 7 y = 0 . You need to convert that equation to a slope equation.

Decision

Let's perform the necessary actions according to the algorithm:

2 x + 7 y = 0 ⇔ 7 y - 2 x ⇔ y = - 2 7 x

Answer: y = - 2 7 x .

From the general equation of a straight line, it is enough to simply obtain an equation in segments of the form x a + y b \u003d 1. To make such a transition, we transfer the number C to the right side of the equality, divide both parts of the resulting equality by - С and, finally, transfer the coefficients for the variables x and y to the denominators:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

Example 8

It is necessary to convert the general equation of the straight line x - 7 y + 1 2 = 0 into the equation of a straight line in segments.

Decision

Let's move 1 2 to the right side: x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

Divide by -1/2 both sides of the equation: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Answer: x - 1 2 + y 1 14 = 1 .

In general, the reverse transition is also easy: from other types of equations to the general one.

The equation of a straight line in segments and the equation with a slope can be easily converted into a general one by simply collecting all the terms on the left side of the equation:

x a + y b ⇔ 1 a x + 1 b y - 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y - k x - b = 0 ⇔ A x + B y + C = 0

The canonical equation is converted to the general one according to the following scheme:

x - x 1 a x = y - y 1 a y ⇔ a y (x - x 1) = a x (y - y 1) ⇔ ⇔ a y x - a x y - a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

To pass from the parametric, first the transition to the canonical is carried out, and then to the general one:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x - x 1 a x = y - y 1 a y ⇔ A x + B y + C = 0

Example 9

The parametric equations of the straight line x = - 1 + 2 · λ y = 4 are given. It is necessary to write down the general equation of this line.

Decision

Let's make the transition from parametric equations to canonical:

x = - 1 + 2 λ y = 4 ⇔ x = - 1 + 2 λ y = 4 + 0 λ ⇔ λ = x + 1 2 λ = y - 4 0 ⇔ x + 1 2 = y - 4 0

Let's move from canonical to general:

x + 1 2 = y - 4 0 ⇔ 0 (x + 1) = 2 (y - 4) ⇔ y - 4 = 0

Answer: y - 4 = 0

Example 10

The equation of a straight line in segments x 3 + y 1 2 = 1 is given. It is necessary to carry out the transition to the general form of the equation.

Decision:

Let's just rewrite the equation in the required form:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y - 1 = 0

Answer: 1 3 x + 2 y - 1 = 0 .

Drawing up a general equation of a straight line

Above, we said that the general equation can be written with known coordinates of the normal vector and the coordinates of the point through which the line passes. Such a straight line is defined by the equation A (x - x 0) + B (y - y 0) = 0 . In the same place we analyzed the corresponding example.

Now let's take a look at more complex examples, in which it is first necessary to determine the coordinates of the normal vector.

Example 11

Given a line parallel to the line 2 x - 3 y + 3 3 = 0 . Also known is the point M 0 (4 , 1) through which the given line passes. It is necessary to write down the equation of a given straight line.

Decision

The initial conditions tell us that the lines are parallel, then, as the normal vector of the line whose equation needs to be written, we take the directing vector of the line n → = (2, - 3) : 2 x - 3 y + 3 3 = 0. Now we know all the necessary data to compose the general equation of a straight line:

A (x - x 0) + B (y - y 0) = 0 ⇔ 2 (x - 4) - 3 (y - 1) = 0 ⇔ 2 x - 3 y - 5 = 0

Answer: 2 x - 3 y - 5 = 0 .

Example 12

The given line passes through the origin perpendicular to the line x - 2 3 = y + 4 5 . It is necessary to write the general equation of a given straight line.

Decision

The normal vector of the given line will be the directing vector of the line x - 2 3 = y + 4 5 .

Then n → = (3 , 5) . The straight line passes through the origin, i.e. through the point O (0, 0) . Let's compose the general equation of a given straight line:

A (x - x 0) + B (y - y 0) = 0 ⇔ 3 (x - 0) + 5 (y - 0) = 0 ⇔ 3 x + 5 y = 0

Answer: 3 x + 5 y = 0 .

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

The solution of the problem usually comes down to finding the value of some quantity by logical reasoning and calculations. For example, find the speed, time, distance, mass of an object or the amount of something.

This problem can be solved using an equation. To do this, the desired value is denoted through a variable, then, by logical reasoning, they compose and solve an equation. Having solved the equation, they check whether the solution of the equation satisfies the conditions of the problem.

Lesson content

Writing Expressions Containing the Unknown

The solution of the problem is accompanied by the compilation of an equation for this problem. On the initial stage studying tasks, it is desirable to learn how to compose literal expressions that describe a particular life situation. This stage is not difficult and can be studied in the process of solving the problem itself.

Consider several situations that can be written using a mathematical expression.

Task 1. Father's age x years. Mom is two years younger. The son is 3 times younger than the father. Record the age of each using expressions.

Decision:

Task 2. Father's age x years, mother is 2 years younger than father. The son is 3 times younger than the father, the daughter is 3 times younger than the mother. Record the age of each using expressions.

Decision:

Task 3. Father's age x years, mother is 3 years younger than father. The son is 3 times younger than the father, the daughter is 3 times younger than the mother. How old is each if the combined age of father, mother, son and daughter is 92?

Decision:

In this problem, in addition to writing expressions, it is necessary to calculate the age of each family member.

First, we write down the age of each family member using expressions. Per variable x let's take the age of the father, and then using this variable we will compose the remaining expressions:

Now let's determine the age of each family member. To do this, we need to write and solve an equation. We have all the components of the equation ready. It remains only to collect them together.

The total age of 92 years was obtained by adding the ages of dad, mom, son and daughter:

For each age, we have mathematical expression. These expressions will be the components of our equation. Let's assemble our equation according to this scheme and the table that was given above. That is, the words dad, mom, son, daughter will be replaced by the expression corresponding to them in the table:

Expression for mother's age x − 3 for clarity, it was taken in brackets.

Now let's solve the resulting equation. To begin with, you can open the brackets where possible:

To free the equation from fractions, multiply both sides by 3

We solve the resulting equation using the known identical transformations:

We found the value of the variable x. This variable was responsible for the age of the father. So the age of the father is 36 years.

Knowing the age of the father, you can calculate the ages of the rest of the family. To do this, you need to substitute the value of the variable x in those expressions that are responsible for the age of a particular family member.

In the problem, it was said that the mother is 3 years younger than the father. We denoted her age through the expression x−3. Variable value x is now known, and in order to calculate the age of the mother, it is necessary in the expression x − 3 instead of x substitute the found value 36

x - 3 \u003d 36 - 3 \u003d 33 years old mom.

Similarly, the age of the remaining family members is determined:

Examination:

Task 4. A kilogram of apples is worth x rubles. Write down an expression that calculates how many kilograms of apples you can buy for 300 rubles.

Decision

If a kilogram of apples costs x rubles, then for 300 rubles you can buy a kilogram of apples.

Example. A kilogram of apples costs 50 rubles. Then for 300 rubles you can buy, that is, 6 kilograms of apples.

Task 5. On the x rubles, 5 kg of apples were bought. Write down an expression that calculates how many rubles one kilogram of apples costs.

Decision

If for 5 kg of apples was paid x rubles, then one kilogram will cost rubles

Example. For 300 rubles, 5 kg of apples were bought. Then one kilogram of apples will cost, that is, 60 rubles.

Task 6. Tom, John and Leo went to the cafeteria during recess and bought a sandwich and a mug of coffee. The sandwich is worth x rubles, and a mug of coffee - 15 rubles. Determine the cost of a sandwich if it is known that 120 rubles were paid for everything?

Decision

Of course, this problem is as simple as three pennies and can be solved without resorting to an equation. To do this, subtract the cost of three cups of coffee (15 × 3) from 120 rubles, and divide the result by 3

But our goal is to write an equation for the problem and solve this equation. So the cost of a sandwich x rubles. Bought only three. So, having tripled the cost, we get an expression describing how many rubles were paid for three sandwiches

3x - cost of three sandwiches

And the cost of three cups of coffee can be written as 15 × 3. 15 is the cost of one mug of coffee, and 3 is a multiplier (Tom, John and Leo) that triples this cost.

According to the condition of the problem, 120 rubles were paid for everything. We already have exemplary scheme, What do we have to do:

We already have expressions describing the cost of three sandwiches and three cups of coffee. These are expressions 3 x and 15×3. Using the scheme, we will write an equation and solve it:

So, the cost of one sandwich is 25 rubles.

The problem is solved correctly only if the equation for it is compiled correctly. Unlike ordinary equations, by which we learn to find roots, equations for solving problems have their own specific application. Each component of such an equation can be described in verbal form. When compiling an equation, it is imperative to understand why we include one or another component in its composition and why it is needed.

It is also necessary to remember that the equation is an equality, after solving which the left side will have to be equal to the right side. The resulting equation should not contradict this idea.

Imagine that the equation is a balance with two bowls and a screen showing the state of the balance.

The screen is currently showing an equals sign. It is clear why the left bowl is equal to the right bowl - there is nothing on the bowls. We write the state of the scales and the absence of something on the bowls using the following equality:

0 = 0

Let's put a watermelon on the left scale:

The left bowl outweighed the right bowl and the screen sounded the alarm, showing the not equal sign (≠). This sign indicates that the left bowl is not equal to the right bowl.

Now let's try to solve the problem. Let it be required to find out how much the watermelon weighs, which lies on the left bowl. But how do you know? After all, our scales are designed only to check whether the left bowl is equal to the right one.

Equations come to the rescue. Recall that by definition the equation is equality A that contains the variable whose value you want to find. The scales in this case play the role of this very equation, and the mass of the watermelon is a variable whose value must be found. Our goal is to get this equation right. Understand, align the scales so that you can calculate the mass of the watermelon.

To level the scales, you can put some heavy object on the right bowl. For example, let's put a weight of 7 kg there.

Now, on the contrary, the right bowl outweighed the left. The screen still shows that the bowls are not equal.

Let's try to put a weight of 4 kg on the left bowl

Now the scales have leveled out. The figure shows that the left bowl is at the level of the right bowl. And the screen shows an equal sign. This sign indicates that the left bowl is equal to the right bowl.

Thus, we have obtained an equation - an equality containing an unknown. The left pan is the left side of the equation, consisting of the 4 components and the variable x(mass of the watermelon), and the right bowl is the right side of the equation, consisting of component 7.

Well, it is not difficult to guess that the root of the equation 4 + x\u003d 7 is 3. So the mass of the watermelon is 3 kg.

The same is true for other tasks. To find some unknown value, various elements are added to the left or right side of the equation: terms, factors, expressions. In school problems, these elements are already given. It remains only to correctly structure them and build an equation. In this example, we were engaged in selection, trying weights of different masses in order to calculate the mass of a watermelon.

Naturally, the data that is given in the problem must first be brought to a form in which they can be included in the equation. Therefore, as they say "Whether you like it or not, you have to think".

Consider the following problem. The age of the father is equal to the age of the son and daughter together. The son is twice as old as the daughter and twenty years younger than the father. How old is each?

The daughter's age can be expressed as x. If the son is twice as old as the daughter, then his age will be indicated as 2 x. The condition of the problem says that together the age of the daughter and son is equal to the age of the father. So the father's age will be denoted by the sum x + 2x

You can add like terms in an expression. Then the father's age will be denoted as 3 x

Now let's make an equation. We need to get an equality in which we can find the unknown x. Let's use weights. On the left bowl we put the age of the father (3 x), and on the right bowl the age of the son (2 x)

It is clear why the left bowl outweighed the right one and why the screen shows the sign (≠) . After all, it is logical that the age of the father is greater than the age of the son.

But we need to balance the scales so that we can calculate the unknown x. To do this, you need to add some number to the right bowl. What number is indicated in the problem. The condition stated that the son was 20 years younger than the father. So 20 years is the same number that needs to be put on the scales.

The scales will even out if we add these 20 years to the right side of the scale. In other words, let's raise the son to the age of the father

Now the scales have leveled out. It turned out the equation , which is easily solved:

x we marked the age of the daughter. Now we have found the value of this variable. Daughter 20 years old.

And finally, we calculate the age of the father. In the problem, it was said that it is equal to the sum of the ages of the son and daughter, that is, (20 + 40) years.

Let's return to the middle of the task and pay attention to one point. When we put the age of the father and the age of the son on the scale, the left bowl outweighed the right

But we solved this problem by adding another 20 years to the right bowl. As a result, the scales leveled out and we got the equality

But it was possible not to add these 20 years to the right bowl, but subtract them from the left. We would get equality in this case

This time the equation is . The root of the equation is still 20

That is, the equations and are equivalent. And we remember that equivalent equations have the same roots. If you look closely at these two equations, you can see that the second equation is obtained by transferring the number 20 from the right side to the left side with the opposite sign. And this action, as indicated in the previous lesson, does not change the roots of the equation.

You also need to pay attention to the fact that at the beginning of solving the problem, the ages of each family member could be denoted through other expressions.

Let's say the son's age is denoted by x and since he is two older than the daughter, then the age of the daughter is indicated by (understand to make her twice as young as the son). And the age of the father, since it is the sum of the ages of the son and daughter, is denoted through the expression . And finally, to build a logically correct equation, you need to add the number 20 to the son’s age, because the father is twenty years older. The result is a completely different equation. . Let's solve this equation

As you can see, the answers to the problem have not changed. My son is still 40 years old. The daughters are still years old, and the father is 40 + 20 years old.

In other words, the problem can be solved in various ways. Therefore, one should not despair that it is not possible to solve this or that problem. But you need to keep in mind that there are the most simple ways to solve the problem. There are various routes to the city center, but there is always the most convenient, fastest and safest route.

Examples of problem solving

Task 1. There are 30 notebooks in two packs. If 2 notebooks were transferred from the first bundle to the second, then there would be twice as many notebooks in the first bundle as in the second. How many notebooks were in each pack?

Decision

Denote by x the number of notebooks that were in the first pack. If there were 30 notebooks in total, and the variable x this is the number of notebooks from the first pack, then the number of notebooks in the second pack will be denoted by the expression 30 − x. That is, from the total number of notebooks, we subtract the number of notebooks from the first pack and thereby obtain the number of notebooks from the second pack.

and add these two notebooks to the second pack

Let's try to make an equation from the existing expressions. We put both packs of notebooks on the scales

The left bowl is heavier than the right. This is because the condition of the problem says that after two notebooks were taken from the first bundle and placed in the second, the number of notebooks in the first bundle became twice as large as in the second.

To equalize the scales and get the equation, double the right side. To do this, multiply it by 2

It turns out an equation. Let's solve this equation:

We denoted the first pack by the variable x. Now we have found its meaning. Variable x equal to 22. So there were 22 notebooks in the first pack.

And we denoted the second pack through the expression 30 − x and since the value of the variable x Now we know, we can calculate the number of notebooks in the second pack. It is equal to 30 − 22, that is, 8 pieces.

Task 2. Two people were peeling potatoes. One peeled two potatoes a minute, and the other three potatoes. Together they cleared 400 pieces. How long did each work if the second worked 25 minutes more than the first?

Decision

Denote by x time of the first person. Since the second person worked 25 minutes more than the first, his time will be denoted by the expression

The first worker peeled 2 potatoes per minute, and since he worked x minutes, then in total he cleared 2 x potatoes.

The second person peeled three potatoes per minute, and since he worked for minutes, he peeled potatoes in total.

Together they peeled 400 potatoes

From the available components, we will compose and solve the equation. On the left side of the equation there will be potatoes peeled by each person, and on the right side of their sum:

At the beginning of the solution of this problem through the variable x we marked the time of work of the first person. Now we have found the value of this variable. The first person worked 65 minutes.

And the second person worked for minutes, and since the value of the variable x now it is known, then you can calculate the time of the second person - it is equal to 65 + 25, that is, 90 minutes.

Problem from Andrey Petrovich Kiselev's Algebra Textbook. A mixture of 32 kg was made from the varieties of tea. A kilogram of the first grade costs 8 rubles, and of the second grade 6 rubles. 50 kop. How many kilograms are taken of both varieties, if a kilogram of the mixture costs (without profit or loss) 7 rubles. 10 kopecks?

Decision

Denote by x a lot of tea of ​​the first grade. Then the mass of tea of ​​the second grade will be denoted through the expression 32 − x

A kilogram of tea of ​​the first grade costs 8 rubles. If these eight rubles are multiplied by the number of kilograms of tea of ​​the first grade, then it will be possible to find out how much the rubles cost x kg of tea of ​​the first grade.

A kilogram of second-class tea costs 6 rubles. 50 kop. If these 6 rubles. 50 kop. multiply by 32 − x, then you can find out how many rubles cost 32 − x kg of tea of ​​the second grade.

The condition says that a kilogram of the mixture costs 7 rubles. 10 kop. In total, 32 kg of the mixture was prepared. Multiply 7 rubles. 10 kop. at 32 we can find out how much 32 kg of the mixture costs.

The expressions from which we will compose the equation now take the following form:

Let's try to make an equation from the existing expressions. Let's put the cost of mixtures of teas of the first and second grades on the left pan of the scales, and put the cost of 32 kg of the mixture on the right pan, that is, the total cost of the mixture, which includes both varieties of tea:

At the beginning of the solution of this problem through the variable x we designated the mass of tea of ​​the first grade. Now we have found the value of this variable. Variable x equals 12.8. This means that 12.8 kg of tea of ​​the first grade was taken to prepare the mixture.

And through expression 32 − x we denoted the mass of tea of ​​the second grade, and since the value of the change x now known, we can calculate the mass of tea of ​​the second grade. It is equal to 32 − 12.8, that is, 19.2. This means that 19.2 kg of second grade tea was taken to prepare the mixture.

Task 3. A cyclist traveled a distance at a speed of 8 km/h. He had to return by another road, which was 3 km longer than the first, and although returning, he was traveling at a speed of 9 km / h, he used time for more than minutes. How long were the roads?

Decision

Some tasks may cover topics that the person may not have studied. This task belongs to such a range of tasks. It deals with the concepts of distance, speed and time. Accordingly, in order to solve such a problem, you need to have an idea about the things that are said in the problem. In our case, we need to know what is the distance, speed and time.

The task is to find the distances of two roads. We must write an equation that will allow us to calculate these distances.

Consider the relationship between distance, speed and time. Each of these quantities can be described using a literal equation:

We will use the right side of one of these equations to draw up our equation. To find out which one, you need to return to the text of the task and pay attention to the following point:

Attention should be paid to the moment where the cyclist on the way back took more than a minute of time. This hint tells us that we can use the equation, namely its right side. This will allow us to write an equation that contains the variable S .

So let's denote the length of the first road as S. The cyclist traveled this path at a speed of 8 km/h. The time for which he covered this path will be denoted by the expression, since time is the ratio of the distance traveled to the speed

The way back for the cyclist was 3 km longer. Therefore, its distance will be denoted by the expression S+ 3 . A cyclist traveled this road at a speed of 9 km/h. So the time for which he overcame this path will be denoted by the expression .

Now let's make an equation from the existing expressions

The right bowl is heavier than the left. This is because the problem says that the cyclist spent more time on the way back.

To equalize the scales, add these same minutes to the left side. But first, let's convert minutes to hours, since in the problem the speed is measured in kilometers per hour, and not in meters per minute.

To convert minutes to hours, you need to divide them by 60

Minutes make hours. Add these hours to the left side of the equation:

It turns out the equation . Let's solve this equation. To get rid of fractions, both parts of the part can be multiplied by 72. Further, using the known identical transformations, we find the value of the variable S

Through a variable S we marked the distance of the first road. Now we have found the value of this variable. Variable S is 15. So the distance of the first road is 15 km.

And we denoted the distance of the second road through the expression S+ 3 , and since the value of the variable S Now we know, we can calculate the distance of the second road. This distance is equal to the sum of 15 + 3, that is, 18 km.

Task 4. Two cars are driving down the highway at the same speed. If the first one increases the speed by 10 km/h, and the second one decreases the speed by 10 km/h, then the first one will cover the same distance in 2 hours as the second one in 3 hours. How fast are the cars?

Decision

Denote by v the speed of each car. Further in the problem, hints are given: increase the speed of the first car by 10 km/h, and decrease the speed of the second car by 10 km/h. Let's use this hint

It is further stated that at such speeds (increased and decreased by 10 km / h), the first car will cover the same distance in 2 hours as the second in 3 hours. Phrase "as many" can be understood as "the distance traveled by the first car will be equals distance traveled by the second car.

The distance, as we remember, is determined by the formula. We are interested in the right side of this literal equation - it will allow us to write an equation containing a variable v .

So, at speed v + 10 km/h the first car will pass 2(v+10) km, and the second will pass 3(v − 10) km. Under this condition, the cars will cover the same distances, so to get the equation, it is enough to connect these two expressions with an equal sign. Then we get the equation. Let's solve it:

In the condition of the problem, it was said that the cars go at the same speed. We denoted this speed by the variable v. Now we have found the value of this variable. Variable v equals 50. So the speed of both cars was 50 km/h.

Task 5. In 9 hours downstream the ship travels the same distance as in 11 hours upstream. Find the speed of the boat if the speed of the river is 2 km/h.

Decision

Denote by v own speed of the ship. The speed of the river flow is 2 km/h. In the course of the river, the speed of the ship will be v + 2 km/h, and against the current - (v − 2) km/h.

The condition of the problem states that in 9 hours the ship travels the same distance along the river as in 11 hours against the current. Phrase "same way" can be understood as the distance traveled by the boat along the river in 9 hours, equals distance traveled by the ship against the current of the river in 11 hours. That is, the distances will be the same.

The distance is determined by the formula . Let's use the right side of this literal equation to write our own equation.

So, in 9 hours, the ship will pass along the river 9(v + 2) km, and in 11 hours upstream - 11(v − 2) km. Since both expressions describe the same distance, we equate the first expression to the second. As a result, we get the equation . Let's solve it:

So the speed of the ship is 20 km/h.

When solving problems, a useful habit is to determine in advance on which solution is sought for it.

Assume that the task required finding the time it would take for a pedestrian to cover a given path. We denoted the time through the variable t, then we made an equation containing this variable and found its value.

From practice, we know that the time of movement of an object can take both integer and fractional values, for example, 2 hours, 1.5 hours, 0.5 hours. Then we can say that the solution to this problem is sought on the set of rational numbers Q, since each of the values ​​2 h, 1.5 h, 0.5 h can be represented as a fraction.

Therefore, after an unknown quantity has been denoted by a variable, it is useful to indicate to which set this quantity belongs. In our example, the time t belongs to the set of rational numbers Q

t ∈ Q

You can also introduce a constraint on the variable t, indicating that it can only take positive values. Indeed, if the object has spent a certain time on the way, then this time cannot be negative. Therefore, next to the expression t∈ Q specify that its value must be greater than zero:

t∈ R, t > 0

If we solve the equation, we get negative meaning for a variable t, then it will be possible to conclude that the problem was solved incorrectly, since this solution will not satisfy the condition t∈ Q , t> 0 .

Another example. If we were solving a problem in which it was required to find the number of people to perform a particular job, then we would denote this number through a variable x. In such a problem, the solution would be sought on the set natural numbers

x ∈ N

Indeed, the number of people is an integer, such as 2 people, 3 people, 5 people. But not 1.5 (one whole person and half a person) or 2.3 (two whole people and another three tenths of a person).

Here one could indicate that the number of people must be greater than zero, but the numbers included in the set of natural numbers N are themselves positive and greater than zero. This set does not negative numbers and the number 0. Therefore, the expression x > 0 can be omitted.

Task 6. To repair the school, a team arrived in which there were 2.5 times more painters than carpenters. Soon the foreman included four more painters in the team, and transferred two carpenters to another object. As a result, there were 4 times more painters in the brigade than carpenters. How many painters and how many carpenters were in the brigade initially

Decision

Denote by x carpenters who arrived for repairs initially.

The number of carpenters is an integer greater than zero. Therefore, we point out that x belongs to the set of natural numbers

x∈N

There were 2.5 times more painters than carpenters. Therefore, the number of painters will be denoted as 2.5x.

And the number of painters will increase by 4

Now the number of carpenters and painters will be denoted by the following expressions:

Let's try to make an equation from the existing expressions:

The right bowl is larger, because after adding four more painters to the team, and moving two carpenters to another object, the number of painters in the team turned out to be 4 times more than carpenters. To equalize the scales, you need to increase the left bowl by 4 times:

Got an equation. Let's solve it:

Through a variable x the initial number of carpenters was designated. Now we have found the value of this variable. Variable x equals 8. So 8 carpenters were in the brigade initially.

And the number of painters was indicated through the expression 2.5 x and since the value of the variable x now it is known, then you can calculate the number of painters - it is equal to 2.5 × 8, that is, 20.

We return to the beginning of the task and make sure that the condition is met x∈ N. Variable x equals 8, and the elements of the set of natural numbers N these are all numbers starting with 1, 2, 3 and so on ad infinitum. The same set includes the number 8, which we found.

8 ∈N

The same can be said about the number of painters. The number 20 belongs to the set of natural numbers:

20 ∈N

To understand the essence of the problem and the correct formulation of the equation, it is not at all necessary to use the model of scales with bowls. You can use other models: segments, tables, diagrams. You can come up with your own model that would describe the essence of the problem well.

Task 9. 30% of milk was poured from the can. As a result, 14 liters remained in it. How many liters of milk were in the can originally?

Decision

The desired value is the initial number of liters in the can. Draw the number of liters as a line and label this line as X

It is said that 30% of the milk was poured out of the can. We select in the figure approximately 30%

A percentage, by definition, is one hundredth of something. If 30% of the milk was poured out, then the remaining 70% remained in the can. These 70% account for 14 liters indicated in the problem. Select the remaining 70% in the figure

Now you can make an equation. Let's remember how to find the percentage of a number. To do this, the total amount of something is divided by 100 and the result is multiplied by the desired percentage. Note that 14 liters, which is 70%, can be obtained in the same way: the initial number of liters X divide by 100 and multiply the result by 70. Equate all this to the number 14

Or get a simpler equation: write 70% as 0.70, then multiply by X and equate this expression to 14

This means that initially there were 20 liters of milk in the can.

Task 9. They took two alloys of gold and silver. In one, the ratio of these metals is 1: 9, and in the other 2: 3. How much of each alloy should be taken to get 15 kg of a new alloy in which gold and silver would be related as 1: 4?

Decision

Let's first try to find out how much gold and silver will be contained in 15 kg of the new alloy. The task says that the content of these metals should be in a ratio of 1: 4, that is, one part of the alloy should be gold, and four parts should be silver. Then the total number of parts in the alloy will be 1 + 4 = 5, and the mass of one part will be 15: 5 = 3 kg.

Let's determine how much gold will be contained in 15 kg of alloy. To do this, multiply 3 kg by the number of parts of gold:

3 kg × 1 = 3 kg

Let's determine how much silver will be contained in 15 kg of alloy:

3 kg × 4 = 12 kg

This means that an alloy weighing 15 kg will contain 3 kg of gold and 12 kg of silver. Now back to the original alloys. You need to use each of them. Denote by x the mass of the first alloy, and the mass of the second alloy can be denoted by 15 − x

Let's express as a percentage all the relationships that are given in the problem and fill in the following table with them:

In the first alloy, gold and silver are in a ratio of 1: 9. Then the total parts will be 1 + 9 = 10. Of these, there will be gold , and silver .

Let's transfer this data to the table. 10% will be entered in the first line in the column "percentage of gold in the alloy", 90% will also be entered in the first line of the column "percentage of silver in the alloy", and in the last column "weight of alloy" enter a variable x, since this is how we denoted the mass of the first alloy:

We do the same with the second alloy. Gold and silver in it are in a ratio of 2: 3. Then there will be 2 + 3 = 5 parts in total. Of these, gold will be , and silver .

Let's transfer this data to the table. 40% will be entered in the second line in the column "percentage of gold in the alloy", 60% will also be entered in the second line of the column "percentage of silver in the alloy", and in the last column "weight of alloy" enter the expression 15 − x, because this is how we denoted the mass of the second alloy:

Let's fill in the last line. The resulting alloy weighing 15 kg will contain 3 kg of gold, which is alloy, and silver will be alloy. In the last column we write down the mass of the resulting alloy 15

You can now write equations using this table. We remember. If we separately add up the gold of both alloys and equate this amount to the mass of gold of the resulting alloy, we can find out what the value is x.

The first gold alloy had 0.10 x, and in the second gold alloy it was 0.40(15 − x) . Then in the resulting alloy, the mass of gold will be the sum of the masses of gold of the first and second alloys, and this mass is 20% of the new alloy. And 20% of the new alloy is 3 kg of gold, calculated by us earlier. As a result, we obtain the equation 0,10x+ 0.40(15 − x) = 3 . Let's solve this equation:

Initially through x we have designated the mass of the first alloy. Now we have found the value of this variable. Variable x is equal to 10. And we denoted the mass of the second alloy through 15 − x, and since the value of the variable x now it is known, then we can calculate the mass of the second alloy, it is equal to 15 − 10 = 5 kg.

This means that to obtain a new alloy weighing 15 kg in which gold and silver would be treated as 1: 4, you need to take 10 kg of the first and 5 kg of the second alloy.

The equation could be made using the second column of the resulting table. Then we would get the equation 0,90x+ 0.60(15 − x) = 12. The root of this equation is also 10

Task 10. There is ore from two layers with a copper content of 6% and 11%. How much low-grade ore should be taken to get it when mixed with rich 20 tons with a copper content of 8%?

Decision

Denote by x mass of poor ore. Since you need to get 20 tons of ore, then 20 rich ore will be taken − x. Since the copper content in poor ore is 6%, then in x tons of ore will contain 0.06 x tons of copper. In rich ore, the copper content is 11%, and in 20 - x tons of rich ore will contain 0.11(20 − x) tons of copper.

In the resulting 20 tons of ore, the copper content should be 8%. This means that 20 tons of copper ore will contain 20 × 0.08 = 1.6 tons.

Add expressions 0.06 x and 0.11(20 − x) and equate this sum to 1.6. We get the equation 0,06x + 0,11(20 − x) = 1,6

Let's solve this equation:

This means that to obtain 20 tons of ore with a copper content of 8%, you need to take 12 tons of poor ore. The rich will take 20 − 12 = 8 tons.

Task 11. Having increased the average speed from 250 to 300 m/min, the athlete began to run the distance 1 minute faster. What is the length of the distance?

Decision

The length of the distance (or the distance of the distance) can be described by the following letter equation:

Let's use the right side of this equation to write our own equation. Initially, the athlete ran the distance at a speed of 250 meters per minute. At this speed, the length of the distance will be described by the expression 250 t

Then the athlete increased her speed to 300 meters per minute. At this speed, the length of the distance will be described by the expression 300t

Note that the length of the distance is a constant value. From the fact that the athlete increases the speed or reduces it, the length of the distance will remain unchanged.

This allows us to equate the expression 250 t to expression 300 t, since both expressions describe the length of the same distance

250t = 300t

But the task says that at a speed of 300 meters per minute, the athlete began to run the distance 1 minute faster. In other words, at a speed of 300 meters per minute, the travel time will decrease by one. Therefore, in equation 250 t= 300t on the right side, the time must be reduced by one:

At a speed of 250 meters per minute, the athlete runs the distance in 6 minutes. Knowing the speed and time, you can determine the length of the distance:

S= 250 × 6 = 1500 m

And at a speed of 300 meters per minute, the athlete runs the distance for t− 1 , that is, in 5 minutes. As mentioned earlier, the length of the distance does not change:

S= 300 × 5 = 1500 m

Task 12. A rider overtakes a pedestrian who is 15 km ahead of him. In how many hours will the rider catch up with the pedestrian if every hour the first rider travels 10 km, and the second travels only 4 km?

Decision

This task is . It can be solved by determining the approach speed and dividing the initial distance between the rider and the pedestrian by this speed.

The closing speed is determined by subtracting the lower speed from the larger one:

10 km/h − 4 km/h = 6 km/h (speed of approach)

Every hour the distance of 15 kilometers will be reduced by 6 kilometers. To find out when it will decrease completely (when the rider catches up with the pedestrian), you need to divide 15 by 6

15:6 = 2.5h

2,5 h it's two whole hours and half an hour. And half an hour is 30 minutes. So the rider will overtake the pedestrian in 2 hours and 30 minutes.

Let's solve this problem using the equation.

After that, after him, a rider set out on the road at a speed of 10 km / h. And the walking speed is only 4 km/h. This means that the rider will overtake the pedestrian after some time. We need to find this time.

When the rider catches up with the pedestrian, it will mean that they have traveled the same distance together. The distance traveled by the rider and the pedestrian is described by the following equation:

Let's use the right side of this equation to write our own equation.

The distance traveled by the rider will be described by the expression 10 t. Since the pedestrian set off before the rider and managed to overcome 15 km, the distance traveled by him will be described by the expression 4 t + 15 .

By the time the rider catches up with the pedestrian, both of them will have covered the same distance. This allows us to equate the distances traveled by the rider and the walker:

The result is a simple equation. Let's solve it:

Tasks for independent solution

Problem 1. A passenger train arrives from one city to another 45 minutes faster than a freight train. Calculate the distance between cities if the speed of the passenger train is 48 km/h, and that of the freight train is 36 km/h.

Decision

The train speeds in this problem are measured in kilometers per hour. Therefore, we will convert the 45 minutes indicated in the task into hours. 45 minutes is 0.75 hours

Let us denote the time during which a freight train arrives in the city through the variable t. Since the passenger train arrives in this city 0.75 hours faster, the time of its movement will be denoted by the expression t - 0,75

Passenger train overcame 48( t - 0.75) km, and commodity 36 t km. Insofar as we are talking about the same distance, we equate the first expression to the second. As a result, we obtain the equation 48(t - 0.75) = 36t . Let's solve it:

Now let's calculate the distance between cities. To do this, the speed of a freight train (36 km / h) is multiplied by the time of its movement t. Variable value t now known - it is equal to three hours

36 × 3 = 108 km

To calculate the distance, you can also use the speed of the passenger train. But in this case the value of the variable

Variable value t equals 1.2. So the cars met after 1.2 hours.

Answer: the cars met after 1.2 hours.

Task 3. There are a total of 685 workers in three workshops of the plant. In the second shop there are three times more workers than in the first, and in the third - 15 workers less than in the second shop. How many workers are in each shop?

Decision

Let be x workers were in the first shop. In the second workshop there were three times more than in the first, so the number of workers in the second workshop can be denoted by the expression 3 x. The third shop had 15 fewer workers than the second. Therefore, the number of workers in the third workshop can be denoted by the expression 3 x - 15 .

The problem says that there were 685 workers in total. Therefore, we can add the expressions x, 3x, 3x - 15 and equate this sum to the number 685. As a result, we obtain the equation x + 3x + ( 3x - 15) = 685

Through a variable x the number of workers in the first workshop was indicated. Now we have found the value of this variable, it is equal to 100. So there were 100 workers in the first shop.

In the second workshop there were 3 x workers, i.e. 3 × 100 = 300. And in the third workshop there were 3 x - 15, i.e. 3 × 100 − 15 = 285

Answer: in the first workshop there were 100 workers, in the second - 300, in the third - 285.

Task 4. Two repair shops within a week should repair 18 motors according to the plan. The first workshop completed the plan by 120%, and the second by 125%, so 22 motors were repaired within a week. What weekly engine repair plan did each workshop have?

Decision

Let be x the motors were to be repaired by the first workshop. Then the second workshop had to renovate 18 − x motors.

Since the first workshop completed its plan by 120%, this means that it has repaired 1.2 x motors. And the second workshop fulfilled its plan by 125%, which means that it repaired 1.25 (18 − x) motors.

The task says that 22 motors were repaired. Therefore, we can add the expressions 1,2x and 1.25(18 − x) , then equate this sum to the number 22. As a result, we obtain the equation 1,2x + 1,25(18− x) = 22

Through a variable x the number of motors that the first workshop was supposed to repair was indicated. Now we have found the value of this variable, it is equal to 10. So the first workshop had to repair 10 motors.

And through the expression 18 − x the number of motors that the second workshop was supposed to repair was indicated. So the second workshop had to repair 18 − 10 = 8 motors.

Answer: the first workshop was to repair 10 motors, and the second 8 motors.

Problem 5. The price of the goods has increased by 30% and is now 91 rubles. How much was the product before the price increase?

Decision

Let be x rubles worth of goods before the price increase. If the price has increased by 30% it means that it has increased by 0.30 x rubles. After the price increase, the goods began to cost 91 rubles. Add x with 0.30 x and equate this sum to 91. As a result, we obtain the equation Decreasing the number by 10% resulted in 45. Find the original value of the number. x -

Answer: to get a 12% salt solution, you need to add 0.25 kg of a 20% solution to 1 kg of a 10% solution.

Problem 12. Two solutions of salt in water are given, the concentrations of which are 20% and 30%. How many kilograms of each solution must be mixed in one vessel to obtain 25 kg of a 25.2% solution?

Decision

Let be x kg of the first solution must be taken. Since it is required to prepare 25 kg of solution, the mass of the second solution can be denoted by the expression 25 − x.

The first solution will contain 0.20x kg of salt, and the second will contain 0.30(25 − x) kg of salt. In the resulting solution, the salt content will be 25 × 0.252 = 6.3 kg. Add the expressions 0.20x and 0.30(25 − x), then equate this sum to 6.3. As a result, we obtain the equation

So the first solution needs to be taken 12 kg, and the second 25 - 12 = 13 kg.

Answer: the first solution you need to take 12 kg, and the second 13 kg.

Did you like the lesson?
Join our new Vkontakte group and start receiving notifications of new lessons

Are you looking for how to write an equation? . A detailed solution with a description and explanations will help you deal with even the most difficult task and make an equation, no exception. We will help you prepare for homework, tests, olympiads, as well as for admission to a university. And no matter what example, no matter what math query you enter, we already have a solution. For example, "how to write an equation."

The use of various mathematical problems, calculators, equations and functions is widespread in our lives. They are used in many calculations, construction of structures and even sports. Mathematics has been used by man since ancient times, and since then their use has only increased. However, now science does not stand still and we can enjoy the fruits of its activities, such as, for example, an online calculator that can solve problems, such as how to write an equation, write an equation. On this page you will find a calculator that will help you solve any question, including how to write an equation. (for example, how to write an equation).

Where can I solve any problem in mathematics, as well as how to make an equation Online?

You can solve the problem of how to write an equation on our website. A free online solver will allow you to solve an online problem of any complexity in a matter of seconds. All you have to do is just enter your data into the solver. You can also watch the video instruction and learn how to correctly enter your task on our website. And if you have any questions, you can ask them in the chat at the bottom left of the calculator page.

To compose an equation means to express in mathematical form the relationship between the data (known) of the problem and the required (unknown) values ​​of it. Sometimes this connection is so clearly contained in the formulation of the problem that the formulation of the equation is simply a literal retelling of the problem, in the language of mathematical signs.

Example 1. Petrov received 160 rubles for his work. more than half of the amount that Ivanov received. Together they received 1120 rubles. How much did Petrov and Ivanov get for their work? Let x be Ivanov's earnings. Half of his earnings are 0.5x; Petrov's monthly salary is 0.5x + 160 together they earn 1120 rubles; the mathematical notation of the last phrase would be

(0.5x + 160) + x = 1120.

The equation has been made. Solving it according to the once established rules, we find Ivanov's earnings x = 640 rubles; Petrov's earnings are 0.5x + 160=480 (rubles).

More often, however, it happens that the relationship between the data and the sought quantities is not directly indicated in the problem; it must be set based on the conditions of the task. In practical problems, this is almost always the case. The example just given is contrived; In real life, such tasks are almost never encountered.

Therefore, it is impossible to give completely exhaustive instructions for compiling an equation. However, at first it is useful to be guided by the following. Let us take for the value of the desired value (or several values) some randomly taken number (or several numbers) and set ourselves the task of checking whether we have guessed correctly correct solution tasks or not. If we were able to carry out this test and find either that our guess is correct or that it is incorrect (the second is most likely to happen, of course), then we can immediately compose desired equation(or several equations). Namely, we will write down the very actions that we performed to check, but instead of a randomly taken number, we will introduce an alphabetic sign of an unknown value. We get the required equation.

Example 2. A piece of an alloy of copper and zinc with a volume of 1 dm3 weighs 8.14 kg. How much copper is in the alloy? (specific weight of copper 8.9 kg/dm3; zinc - 7.0 kg/dm3).

Let us take at random a number expressing the desired volume of copper, for example, 0.3 dm3. Let's check if we have successfully taken this number. Since 1 kg / dm3 of copper weighs 8.9 kg, then 0.3 dm3 weighs 8.9 * 0.3 = 2.67 (kg). The volume of zinc in the alloy is 1 - 0.3 = 0.7 (dm3). Its weight is 7.0 0.7 = 4.9 (kg). The total weight of zinc and copper is 2.67 + + 4.9 = 7.57 (kg). Meanwhile, the weight of our piece, according to the condition of the problem, is 8.14 kg. Our guess is invalid. But on the other hand, we will immediately get an equation whose solution will give the correct answer. Instead of a randomly taken number of 0.3 dm3, we denote the volume of copper (in dm3) through x. Instead of the product 8.9 0.3 = 2.67 we take the products 8.9 x. This is the weight of the copper in the alloy. Instead of 1 - 0.3 = 0.7 we take 1 - x; this is the amount of zinc. Instead of 7.0 0.7 = 4.9 we take 7.0 (1 - x); this is the weight of zinc. Instead of 2.67 + 4.9 we take 8.9 x + 7.0 (1 - x); this is the combined weight of zinc and copper. By condition, it is equal to 8.14 kg; so 8.9 x + 7.0 (1 - x) = 8.14.

Solving this equation gives x = 0.6. Checking a randomly chosen solution can be done in various ways; accordingly, for the same problem, different types of equations can be obtained; all of them, however, will give the same solution for the desired value, such equations are called equivalent to each other.

Of course, after gaining skills in compiling equations, there is no need to randomly check the number taken: you can take for the value of the desired value not a number, but some letter (x, y, etc.) and act as if this letter ( unknown) was the number we are going to test.