ОРТ (единичный вектор). Векторы и операции над векторами Найти координаты орта вектора

Единичный вектор - это вектор , абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а , то его единичным вектором будет вектор а е. Этот единичный вектор направлен туда же, куда направлен и сам вектор а , и его модуль равен единице, то есть а е = 1.

Очевидно, а = а·а е (а - модуль вектора а) . Это следует из правила, по которому выполняется операция умножения скаляра на вектор .

Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

Напомню, что декартовой системой координат в пространстве традиционно называется тройка взаимно перпендикулярных осей, пересекающихся в точке, которая называется началом координат. Координатные оси обычно обозначают буквами X , Y , Z и называют соответственно осью абсцисс, осью ординат и осью аппликат. Сам Декарт пользовался только одной осью, на которой откладывались абсциссы. Заслуга использования системы осей принадлежит его ученикам. Поэтому фраза декартова система координат исторически ошибочна. Лучше говорить прямоугольная система координат или ортогональная система координат . Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат - это одно и то же.

Единичный вектор , направленный вдоль оси Х, обозначается i , единичный вектор , направленный вдоль оси Y , обозначается j , а единичный вектор , направленный вдоль оси Z, обозначается k . Векторы i , j , k называются ортами (рис. 12, слева), они имеют единичные модули, то есть
i = 1, j = 1, k = 1.

Оси и орты прямоугольной системы координат в некоторых случаях имеют другие названия и обозначения. Так, ось абсцисс X может называться касательной осью, а ее орт обозначается τ (греческая строчная буква тау), ось ординат - осью нормали, ее орт обозначается n , ось аппликат - осью бинормали, ее орт обозначается b . Зачем менять названия, если суть остается той же?

Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k .

Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i , а τ . Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности - к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль - это одно и то же). Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это - бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие вектора

Прежде чем Вы узнаете всё о векторах и операциях над ними, настройтесь на решение несложной задачи. Есть вектор Вашей предприимчивости и вектор Ваших инновационных способностей. Вектор предприимчивости ведёт Вас к Цели 1, а вектор инновационных способностей - к Цели 2. Правила игры таковы, что Вы не можете двигаться сразу по направлениям двух этих векторов и достигнуть сразу двух целей. Векторы взаимодействуют, или, если говорить математическим языком, над векторами производится некоторая операция. Результатом этой операции становится вектор "Результат", который приводит Вас к Цели 3.

А теперь скажите: результатом какой операции над векторами "Предприимчивость" и "Инновационные способности" является вектор "Результат"? Если не можете сказать сразу, не унывайте. По мере изучения этого урока Вы сможете ответить на этот вопрос.

Как мы уже увидели выше, вектор обязательно идёт от некоторой точки A по прямой к некоторой точке B . Следовательно, каждый вектор имеет не только числовое значение - длину, но также физическое и геометрическое - направленность. Из этого выводится первое, самое простое определение вектора. Итак, вектор - это направленный отрезок, идущий от точки A к точке B . Обозначается он так: .

А чтобы приступить к различным операциям с векторами , нам нужно познакомиться с ещё одним определением вектора.

Вектор - это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z ) . Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.

Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.

Все остальные термины - это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.

Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.

Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка . Это отрезок, у которого различают начало и конец.

Если A - начало вектора, а B - его конец, то вектор обозначается символом или одной строчной буквой . На рисунке конец вектора указывается стрелкой (рис. 1)

Длиной (или модулем ) геометрического вектора называется длина порождающего его отрезка

Два вектора называются равными , если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.

В физике часто рассматриваются закреплённые векторы , заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным . Мы договоримся рассматривать только свободные векторы .

Линейные операции над геометрическими векторами

Умножение вектора на число

Произведением вектора на число называется вектор, получающийся из вектора растяжением (при ) или сжатием (при ) в раз, причём направление вектора сохраняется, если , и меняется на противоположное, если . (Рис. 2)

Из определения следует, что векторы и = всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными . (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить "коллинеарны".) Справедливо и обратное утверждение: если векторы и коллинеарны, то они связаны отношением

Следовательно, равенство (1) выражает условие коллинеарности двух векторов.

Сложение и вычитание векторов

При сложении векторов нужно знать, что суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец - с концом вектора , при условии, что начало вектора приложено к концу вектора . (Рис. 3)

Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n свободных векторов . При сложении нескольких векторов за их сумму принимают замыкающий вектор, начало которого совпадает с началом первого вектора, а конец - с концом последнего вектора. То есть, если к концу вектора приложить начало вектора , а к концу вектора - начало вектора и т.д. и, наконец, к концу вектора - начало вектора , то суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора , а конец - с концом последнего вектора . (Рис. 4)

Слагаемые называются составляющими вектора , а сформулированное правило - правилом многоугольника . Этот многоугольник может и не быть плоским.

При умножении вектора на число -1 получается противоположный вектор . Векторы и имеют одинаковые длины и противоположные направления. Их сумма даёт нулевой вектор , длина которого равна нулю. Направление нулевого вектора не определено.

В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора вектор означает прибавить к вектору противоположный вектор , т.е.

Пример 1. Упростить выражение:

.

,

то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.

Пример 2. Векторы и служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через и векторы , , и , являющиеся сторонами этого параллелограмма.

Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат - требуемые в условии задачи векторы:

Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах "Предприимчивость" и "Инновационные способности" в начале этого урока. Правильный ответ: над этими векторами производится операция сложения.

Решить задачи на векторы самостоятельно, а затем посмотреть решения

Как найти длину суммы векторов?

Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:

Даны длины векторов и длина суммы этих векторов . Найти длину разности этих векторов .

Решения этой и других подобных задач и объяснения, как их решать - в уроке "Сложение векторов: длина суммы векторов и теорема косинусов ".

А проверить решение таких задач можно на Калькуляторе онлайн "Неизвестная сторона треугольника (сложение векторов и теорема косинусов)" .

А где произведения векторов?

Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки "Скалярное произведение векторов " и "Векторное и смешанное произведения векторов ".

Проекция вектора на ось

Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

Как известно, проекцией точки A на прямую (плоскость) служит основание перпендикуляра , опущенного из этой точки на прямую (плоскость).

Пусть - произвольный вектор (Рис. 5), а и - проекции его начала (точки A ) и конца (точки B ) на ось l . (Для построения проекции точки A ) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.

Составляющей вектора на оси l называется такой вектор , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец - с проекцией конца вектора .

Проекцией вектора на ось l называется число

,

равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l , и со знаком минус, если эти направления противоположны.

Основные свойства проекций вектора на ось:

1. Проекции равных векторов на одну и ту же ось равны между собой.

2. При умножении вектора на число его проекция умножается на это же число.

3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.

4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:

.

Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:

Находим окончательную проекцию суммы векторов:

Связь вектора с прямоугольной декартовой системой координат в пространстве

Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке , желательно открыть его в новом окне.

В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс , ось 0y – осью ординат , и ось 0z – осью аппликат .

С произвольной точкой М пространства свяжем вектор

называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:

Числа x, y, z называются координатами точки М , соответственно абсциссой , ординатой и аппликатой , и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).

Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором (или ортом ) оси. Обозначим через

Соответственно орты координатных осей Ox , Oy , Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей:

(2)

Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.

После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме

Представления вектора в виде (2) и (3) тождественны.

Условие коллинеарности векторов в координатах

Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением

Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением

,

то есть, координаты векторов пропорциональны.

Пример 6. Даны векторы . Коллинеарны ли эти векторы?

Решение. Выясним соотношение координат данных векторов:

.

Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.

Длина вектора и направляющие косинусы

Вследствие взаимной перпендикулярности координатных осей длина вектора

равна длине диагонали прямоугольного параллелепипеда, построенного на векторах

и выражается равенством

(4)

Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.

Пусть в заданной системе координат начало вектора находится в точке

а конец – в точке

Из равенства

Следует, что

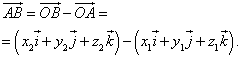
или в координатной форме

Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора . Формула (4) в этом случае примет вид

Направление вектора определяют направляющие косинусы . Это косинусы углов, которые вектор образует с осями Ox , Oy и Oz . Обозначим эти углы соответственно α , β и γ . Тогда косинусы этих углов можно найти по формулам

Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора

.

Учитывая, что длина орта вектора равна одной единице, то есть

,

получаем следующее равенство для направляющих косинусов:

Пример 7. Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

Пример 8. Даны точки:

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:

Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.

Пример 9. Найти длину вектора и его направляющие косинусы, если .

Решение. Координаты вектора даны:

.

Длина вектора равна квадратному корню из суммы квадратов координат вектора:

.

Находим направляющие косинусы:

Решить задачу на векторы самостоятельно, а затем посмотреть решение

Операции над векторами, заданными в координатной форме

Пусть даны два вектора и , заданные своими проекциями:

Укажем действия над этими векторами.

Изменение координаты x2 — x1 принято обозначать символом Δx12 (читается «дельта икс один, два»). Эта запись означает, что за промежуток времени от момента t1 до момента t2 изменение координаты тела Δx12 = x2 — x1. Таким образом, если тело двигалось в положительном направлении оси X выбранной системы координат (x2 > x1), то Δx12 >

На рис. 45 изображено точечное тело В, которое движется в отрицательном направлении оси X. За промежуток времени от t1 до t2 оно перемещается из точки с большей координатой x1 в точку с меньшей координатой x2. В результате изменение координаты точки B за рассматриваемый промежуток времени Δx12 = x2 — x1 = (2 — 5) м = -3 м. Вектор перемещения в этом случае будет направлен в отрицательном направлении оси X, а его модуль |Δx12| равен 3 м. Из рассмотренных примеров можно сделать следующие выводы.

В рассмотренных примерах (см. рис. 44 и 45) тело все время двигалось в каком-либо одном направлении.

Как найти модуль перемещения в физике?(может есть какая-нибудь универсальная формула?)

Поэтому пройденный им путь равен модулю изменения координаты тела и модулю перемещения: s12 = |Δx12|.

Определим изменение координаты и перемещение тела за промежуток времени от t0 = 0 до t2 = 7 с. В соответствии с определением изменение координаты Δx02 = x2 — x0 = 2 м >

Теперь определим путь, который прошло тело за тот же промежуток времени от t0 = 0 до t2 = 7 с. Сначала тело прошло 8 м в одном направлении (что соответствует модулю изменения координаты Δx01), а затем 6 м в обратном направлении (эта величина соответствует модулю изменения координаты Δx12). Значит, всего тело прошло 8 + 6 = 14 (м). По определению пути за промежуток времени от t0 до t2 тело прошло путь s02 = 14 м.

Итоги

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки.

Вопросы

Упражнения

Векторы, действия с векторами

теоремы Пифагора теореме косинусов

Длину вектора будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

, откуда .

Таким образом, .

Рассмотрим пример.

:

.

Таким образом, длина вектора .

Вычислите длину вектора

, следовательно,

К началу страницы

Рассмотрим решения примеров.

.

Перемещение

:

:

.

.

К началу страницы

Таким образом, .

или ,
или ,

Некогда разбираться?
Закажите решение

К началу страницы

До сих пор мы рассматривали только прямолинейное равномерное движение. При этом точечные тела двигались в выбранной системе отсчета либо в положительном, либо в отрицательном направлении оси координат X. Мы установили, что в зависимости от направления движения тела, например, за промежуток времени от момента t1 до момента t2 изменение координаты тела (x2 — x1) может быть положительным, отрицательным или равным нулю (если x2 = x1).

Изменение координаты x2 — x1 принято обозначать символом Δx12 (читается «дельта икс один, два»). Эта запись означает, что за промежуток времени от момента t1 до момента t2 изменение координаты тела Δx12 = x2 — x1. Таким образом, если тело двигалось в положительном направлении оси X выбранной системы координат (x2 > x1), то Δx12 > 0. Если же движение происходило в отрицательном направлении оси X (x21), то Δx12

Результат движения удобно определять с помощью векторной величины. Такой векторной величиной является перемещение.

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки.

Как и любую векторную величину, перемещение характеризуют модулем и направлением.

Записывать вектор перемещения точки за промежуток времени от t1 до t2 мы будем следующим способом: Δx12.

Поясним сказанное на примере. Пусть некоторая точка A (точечное чело) движется в положительном направлении оси X и за промежуток времени от t1 до t2 перемещается из точки с координатой x1 в точку с большей координатой x2 (рис. 44). В этом случае вектор перемещения направлен в положительном направлении оси X, а его модуль равен изменению координаты за рассматриваемый промежуток времени: Δx12 = x2 — x1 = (5 — 2) м = 3 м.

На рис. 45 изображено точечное тело В, которое движется в отрицательном направлении оси X.

За промежуток времени от t1 до t2 оно перемещается из точки с большей координатой x1 в точку с меньшей координатой x2. В результате изменение координаты точки B за рассматриваемый промежуток времени Δx12 = x2 — x1 = (2 — 5) м = -3 м. Вектор перемещения в этом случае будет направлен в отрицательном направлении оси X, а его модуль |Δx12| равен 3 м. Из рассмотренных примеров можно сделать следующие выводы.

Направление перемещения при прямолинейном движении в одном направлении совпадает с направлением движения.

Модуль вектора перемещения равен модулю изменения координаты тела за рассматриваемый промежуток времени.

В повседневной жизни для описания конечного результата движения используют понятие «путь». Обычно путь обозначают символом S.

Путь – это все расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Как и любое расстояние, путь – величина неотрицательная. Например, путь, пройденный точкой A в рассмотренном примере (см. рис. 44), равен трем метрам. Путь, пройденный точкой B, также равен трем метрам.

В рассмотренных примерах (см. рис. 44 и 45) тело все время двигалось в каком-либо одном направлении. Поэтому пройденный им путь равен модулю изменения координаты тела и модулю перемещения: s12 = |Δx12|.

Если тело двигалось все время в одном направлении, то пройденный им путь равен модулю перемещения и модулю изменения координаты.

Ситуация изменится, если тело в течение рассматриваемого промежутка времени изменяет направление движения.

На рис. 46 изображено, как двигалось точечное тело с момента t0 = 0 до момента t2 = 7 с. До момента t1 = 4 с движение происходило равномерно в положительном направлении оси X. В результате чего изменение координаты Δx01 = x1 — x0 = (11 — 3) м = -8 м. После этого тело стало двигаться в отрицательном направлении оси X до момента t2 = 7 с. При этом изменение его координаты Δx12 = x2 — x1 = (5 — 11) м = -6 м. График этого движения приведен на рис. 47.

Определим изменение координаты и перемещение тела за промежуток времени от t0 = 0 до t2 = 7 с. В соответствии с определением изменение координаты Δx02 = x2 — x0 = 2 м > 0. Поэтому перемещение Δx02 направлено в положительном направлении оси Х, а его модуль равен 2 м.

Теперь определим путь, который прошло тело за тот же промежуток времени от t0 = 0 до t2 = 7 с. Сначала тело прошло 8 м в одном направлении (что соответствует модулю изменения координаты Δx01), а затем 6 м в обратном направлении (эта величина соответствует модулю изменения координаты Δx12).

Траектория

Значит, всего тело прошло 8 + 6 = 14 (м). По определению пути за промежуток времени от t0 до t2 тело прошло путь s02 = 14 м.

Разобранный пример позволяет сделать вывод:

В случае, когда тело в течение рассматриваемого промежутка времени меняет направление своего движения, путь (все пройденное телом расстояние) больше и модуля перемещения тела, и модуля изменения координаты тела.

Теперь представьте себе, что тело после момента времени t2 = 7 с продолжило свое движение в отрицательном направлении оси X до момента t3 = 8 с в соответствии с законом, изображенным на рис. 47 пунктирной линией. В результате в момент времени t3 = 8 с координата тела стала равна x3 = 3 м. Нетрудно определить, что в этом случае перемещение тела за промежуток времени от t0 до t3 с равно Δx13 = 0.

Ясно, что если нам известно только перемещение тела за время его движения, то мы не можем сказать как двигалось тело в течение этого времени. Например, если бы о теле было известно только, что его начальная и конечная координаты равны, то мы сказали бы, что за время движения перемещение этого тела равно нулю. Сказать что-либо более конкретное о характере движения этого тела было бы нельзя. Тело могло при таких условиях вообще стоять на месте в течение всего промежутка времени.

Перемещение тела за некоторый промежуток времени зависит только от начальной и конечной координат тела и не зависит от того, как двигалось тело в течение этого промежутка времени.

Итоги

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки.

Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь – все расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения.

Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и молуля перемещения тела, и модуля изменения координаты тела.

Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).

Вопросы

1. Что такое перемещение? От чего оно зависит?
2. Что такое путь? От чего он зависит?
3. Чем путь отличается от перемещения и изменения координаты за один и тот же промежуток времени, в течение которого тело двигалось прямолинейно, не изменяя направления движения?

Упражнения

1. Используя закон движения в графической форме, представленный на рис. 47, опишите характер движения тела (направление, скорость) в разные промежутки времени: от t0 до t1, от t1 до t2, от t2 до t3.
2. Собачка Протон выбежала из дома в момент времени t0 = 0, а затем по команде своего хозяина в момент времени t4 = 4 с бросилась обратно. Зная, что Протон все время бежал по прямой и модуль его скорости |v| = 4 м/с, определите графическим способом: а) изменение координаты и путь Протона за промежуток времени от t0 = 0 до t6 = 6 с; б) путь Протона за промежуток времени от t2 = 2 с до t5 = 5 с.

Векторы, действия с векторами

Нахождение длины вектора, примеры и решения.

По определению вектор – это направленный отрезок, а длина этого отрезка в заданном масштабе является длиной вектора. Таким образом, задача нахождения длины вектора на плоскости и в пространстве сводится к нахождению длины соответствующего отрезка. Для решения этой задачи в нашем распоряжении все средства геометрии, хотя в большинстве случаев достаточно теоремы Пифагора . С ее помощью можно получить формулу для вычисления длины вектора по его координатам в прямоугольной системе координат, а также формулу нахождения длины вектора по координатам точек его начала и конца. Когда вектор является стороной треугольника, то его длина может быть найдена по теореме косинусов , если известны длины двух других сторон и угол между ними.

Нахождение длины вектора по координатам.

Длину вектора будем обозначать .

физический словарик (кинематика)

Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координатOxy. Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координат мы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.

Рассмотрим пример.

Найдите длину вектора , заданного в декартовой системе координат.

Сразу применяем формулу для нахождения длины вектора по координатам :

Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .

Вычислите длину вектора , где — орты прямоугольной системы координат.

Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

К началу страницы

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Таким образом, если на плоскости заданы точки и , то вектор имеет координаты и его длина вычисляется по формуле , а формула для нахождения длины вектора по координатам точек и трехмерного пространства имеет вид .

Рассмотрим решения примеров.

Найдите длину вектора , если в прямоугольной декартовой системе координат .

Можно сразу применить формулу для нахождения длины вектора по координатам точек начала и конца на плоскости :

Вторым вариантом решения является определение координат вектора через координаты точек и применение формулы :

.

Определите, при каких значениях длина вектора равна , если .

Длина вектора по координатам точек начала и конца может быть найдена как

Приравняв полученное значение длины вектора к , вычислим искомые :

К началу страницы

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов , и угол между ними (или косинус угла), а требуется найти длину вектора или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Длины векторов и равны 3 и 7 соответственно, а угол между ними равен . Вычислите длину вектора .

Длина вектора равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:

Таким образом, .

Итак, для нахождения длины вектора по координатам используем формулы
или ,
по координатам точек начала и конца вектора —
или ,
в некоторых случаях к результату приводит теорема косинусов.

Некогда разбираться?
Закажите решение

К началу страницы

• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.

Поиск Лекций

Скалярный квадрат вектора

Что будет, если вектор умножить на самого себя?

Число называется скалярным квадратом вектора , и обозначатся как .

Таким образом,скалярный квадрат вектора равен квадрату длины данного вектора:

Вектором в геометрии называют направленный отрезок или упорядоченную пару точек евклидова пространства.Ортом вектора является единичный вектор нормированного векторного пространства или вектор, норма (длина) которого равна единице.

Вам понадобится

• Знания по геометрии.

Инструкция

Для начала необходимо вычислить длину вектора . Как известно, длина (модуль) вектора равна корню квадратному из суммы квадратов координат. Пусть дан вектор с координатами: a(3, 4). Тогда его длина равна |a| = (9 + 16)^1/2 или |a|=5.

Чтобы найти орт вектора a, необходимо поделить каждую его на его длину. Результатом будет вектор, который называется ортом или единичным вектором. Для вектора а(3, 4) ортом будет являться вектор а(3/5, 4/5). Вектор a` будет являться единичным для вектора а.

Для проверки, правильно ли найден орт, можно проделать следующее: найти длину полученного орта, если она равна единице, то все найдено верно, если нет, то в расчеты закралась ошибка. Проверим правильно ли найден орт a`. Длина вектора a` равна: a` = (9/25 + 16/25)^1/2 = (25/25)^1/2 = 1. Итак, длина вектора a` равна единице, значит орт найден верно.