Cum să înțelegeți că o funcție este periodică. Funcția periodică. Exemple de funcții periodice și graficele acestora
Cererea nr. 7
Instituție de învățământ municipală
in medie şcoală cuprinzătoare № 3
Profesor
Korotkov
Asya Edikovna
Kurganinsk
2008
CONŢINUT
Introducere ……………………………………………………… 2-3
Funcțiile periodice și proprietățile lor ……………. 4-6
Sarcini ……………………………………………………… 7-14
Introducere
De remarcat că problemele de periodicitate din literatura educațională și metodologică au o soartă dificilă. Acest lucru se explică printr-o tradiție ciudată - de a permite una sau alta neglijență în definirea funcțiilor periodice care duc la decizii controversate și provoacă incidente la examene.
De exemplu, în carte Dicţionar termeni matematici "- M, 1965, este dată următoarea definiție:" o funcție periodică - o funcție
y = f(x), pentru care există un număr t > 0, care pentru toate x și x + t din domeniul f(x + t) = f(x).
Să dăm un contra-exemplu care arată incorectitudinea acestei definiții. Conform acestei definiții, funcția este periodică cu perioada t = 2π
с(x) = Cos(√x) 2 – Cos(√4π - x) 2 cu un domeniu limitat de definiție, ceea ce contrazice punctul de vedere general acceptat despre funcțiile periodice.
Probleme similare apar în multe dintre cele mai noi manuale alternative pentru școală.
Manualul lui A. N. Kolmogorov dă următoarea definiție: „Vorbind despre periodicitatea funcției f, se crede că există un astfel de număr T ≠ 0 încât domeniul definiției D (f) împreună cu fiecare punct x conține puncte care se obțin din x prin translație paralelă de-a lungul axei Ox (dreapta și stânga) cu o distanță T. Se numește funcția f periodic cu perioada T ≠ 0, dacă pentru oricare dintre domeniile de definiție valorile acestei funcții în punctele x, x - T, x + T sunt egale, adică. f (x + T) \u003d f (x) \u003d f (x - T) ". Mai departe în manual este scris: „Deoarece sinusul și cosinusul sunt definite pe întreaga dreaptă numerică și Sin (x + 2π) = Sin x,
Cos (x + 2π) \u003d Cos x pentru orice x, sinus și cosinus sunt perioada unei funcții cu o perioadă de 2π.
Din anumite motive, acest exemplu nu verifică ceea ce se cere în definiția condiției care
Sin (x - 2π) \u003d Sin x. Ce s-a întâmplat? Ideea este că această condiție este de prisos în definiție. Într-adevăr, dacă T > 0 este perioada funcției f(x), atunci T va fi și perioada acestei funcție.
Vreau să mai dau o definiție din manualul lui M.I. Bashmakov „Algebra și începutul analizei în 10-11 celule”. „Funcția y \u003d f (x) se numește periodică dacă există un astfel de număr T ≠ 0 încât egalitatea
f(x + T) = f(x) este valabil pentru toate valorile lui x.
Definiția de mai sus nu spune nimic despre domeniul de aplicare al funcției, deși înseamnă x din domeniul de aplicare al definiției, nu orice x real. Conform acestei definiții, funcția y \u003d Sin (√x) poate fi periodică 2 , definit doar pentru x ≥ 0, ceea ce nu este adevărat.
În examenul de stat unificat există sarcini pentru periodicitate. Într-un jurnal științific periodic, ca pregătire pentru secțiunea C a examenului unificat de stat, a fost dată soluția problemei: „este funcția y (x) \u003d Sin 2 (2 + x) - 2 Sin 2 Sin x Cos (2 + x) periodic?
Soluția arată că y (x - π) \u003d y (x) în răspuns - o intrare suplimentară
„T = π” (la urma urmei, nu se pune problema găsirii celei mai mici perioade pozitive). Este cu adevărat necesar să se efectueze o formație trigonometrică complexă pentru a rezolva această problemă? La urma urmei, aici vă puteți concentra pe conceptul de periodicitate, ca cheie în starea problemei.
Decizie.
f1 (x) \u003d Sin x - o funcție periodică cu o perioadă T \u003d 2π
f2 (x) = Cos x este o funcție periodică cu perioada T = 2π, atunci 2π este o perioadă și pentru funcțiile f 3(x) = Sin(2+x) și f 4 (x) = Cos (2 + x), (aceasta rezultă din definiția periodicității)
f5 (x) = - 2 Sin 2 = Const, perioada sa este orice număr, inclusiv 2π.
pentru că suma și produsul funcțiilor periodice cu o perioadă comună T este și T-periodic, atunci această funcție este periodică.
Sper că materialul prezentat în această lucrare va ajuta la pregătirea unui singur examen de statîn rezolvarea problemelor de periodicitate.
Funcții periodice și proprietățile lor
Definiție: o funcție f(t) se numește periodică dacă pentru orice t din domeniul de definire al acestei funcții D f există un număr ω ≠ 0 astfel încât:
1) numere (t ± ω) є D f ;
2) f(t + ω) = f(t).
1. Dacă numărul ω = perioada funcției f (t), atunci numărul kω, unde k = ±1, ±2, ±3, … sunt și perioadele funcției f(t).
EXEMPLU f(t) = Sint. Numărul T = 2π este cea mai mică perioadă pozitivă a acestei funcții. Fie T 1 = 4π. Să arătăm că T 1 este și perioada acestei funcții.
F (t + 4π) = f (t + 2π + 2π) = Sin (t + 2π) = Sin t.
Deci T 1 este perioada funcției f (t) = Sin t.
2. Dacă funcția f(t) - ω este o funcție periodică, atunci funcțiile f (at), unde a є R, și f (t + c), unde c este o constantă arbitrară, sunt și ele periodice.
Aflați perioada funcției f(аt).
f(аt) = f(аt + ω) = f (а(t + ω/а)), adică. f (аt) = f (а(t + ω/а).
Prin urmare, perioada funcției f(аt) – ω 1 = ω/а.
EXEMPLU 1. Aflați perioada funcției y = Sin t/2.
Exemplul 2. Găsiți perioada funcției y \u003d Sin (t + π / 3).
Fie f(t) = Sin t; y 0 \u003d Sin (t 0 + π / 3).
Atunci funcția f(t) = Sin t va lua și valoarea y 0 pentru t = t 0 + π/3.
Acestea. toate valorile pe care le ia funcția y sunt luate și de funcția f(t). Dacă t este interpretat ca timp, atunci fiecare valoare a lui y 0 funcția y \u003d Sin (t + π / 3) este luată cu π / 3 unități de timp mai devreme decât funcția f (t) "deplasare" la stânga cu π / 3. Evident, perioada funcției nu se va schimba de la aceasta, adică. T y \u003d T 1.
3. Dacă F(x) este o funcție și f(t) este o funcție periodică astfel încât f(t) aparține domeniului funcției F(x) – D F , atunci funcția F(f (t)) este o funcție periodică.
Fie F(f (t)) = φ.
Φ (t + ω) = F(f (t + ω)) = F(f (t)) = φ (t) pentru orice t є D f.
EXEMPLU Investigați funcția pentru periodicitate: F(x) = ℓ sin x .
Scopul acestei funcții D f coincide cu multimea numerelor reale R. f (x) = Sin x.
Setul de valori ale acestei funcții este [-1; unu]. pentru că segmentul [-1; 1] aparține lui D f , atunci funcția F(x) este periodică.
F(x+2π) = ℓ sin (x + 2π) = ℓ sin x = F(x).
2 π este perioada acestei funcții.
4. Dacă funcţiile f 1 (t) şi f 2 (t) periodic, respectiv, cu perioade ω 1 și ω 2 și ω 1 / ω 2 = r, unde r este un număr rațional, apoi funcțiile
С 1 f 1 (t) + С 2 f 2 (t) și f 1 (t) f 2 (t) sunt periodice (~ 1 și C 2 sunt constante).
Notă: 1) Dacă r = ω 1 /ω 2 = p/q, deoarece r este un număr rațional, atunci
ω 1 q = ω 2 p = ω, unde ω este cel mai mic multiplu comun al numerelor ω 1 și ω2 (LCM).
Luați în considerare funcția C 1 f 1 (t) + C 2 f 2 (t).
Într-adevăr, ω = LCM (ω 1, ω 2 ) - perioada acestei funcții
С 1 f 1 (t) + С 2 f 2 (t) = С 1 f 1 (t+ ω 1 q) + С 2 f 2 (t+ ω 2 p) + С 1 f 1 (t) + С 2 f 2 (t).
2) ω este perioada funcției f 1 (t) f 2 (t), deoarece
f 1 (t + ω) f 2 (t + ω \u003d f 1 (t + ω 1 q) f 2 (t \u003d ω 2 p) \u003d f 1 (t) f 2 (t).
Definiție: Fie f 1 (t) și f (t) sunt funcții periodice cu perioade, respectiv ω 1 și ω 2 , atunci se spune că două perioade sunt comparabile dacăω 1 / ω 2 = r este un număr rațional.
3) Dacă perioadele ω 1 și ω 2 nu sunt comensurabile, atunci funcțiile f 1 (t) + f 2 (t) și
f 1 (t) f 2 (t) nu sunt periodice. Adică dacă f 1 (t) și f 2 (t) sunt diferite de o constantă, periodică, continuă, perioadele lor nu sunt proporționale, atunci f 1 (t) + f 2 (t), f 1 (t) f 2 (t) nu sunt periodice.
4) Fie f(t) = С, unde С este o constantă arbitrară. Această funcție este periodică. Perioada sa este orice număr rațional, ceea ce înseamnă că nu are cea mai mică perioadă pozitivă.
5) Afirmația este valabilă și pentru mai multe funcții.
Exemplul 1. Investigați periodicitatea funcției
F(x) = Sin x + Cos x.
Decizie. Fie f 1 (x) = Sin x, apoi ω 1 = 2πk, unde k є Z.
T 1 = 2π este cea mai mică perioadă pozitivă.
f 2 (x) \u003d Cos x, T 2 \u003d 2π.
Raportul T 1 /T 2 = 2π/2π = 1 este un număr rațional, adică. perioade de funcții f 1 (x) și f 2 (x) sunt proporționale. Deci această funcție este periodică. Să-i găsim perioada. Prin definiția unei funcții periodice, avem
Sin (x + T) + Cos (x + T) = Sin x + Cos x,
Sin (x + T) - Sin x \u003d Cos x - Cos (x + T),
2 Cos 2x + π / 2 Sin T / 2 \u003d 2 Sin 2x + T / 2 Sin T / 2,
Sin T / 2 (Cos T + 2x / 2 - Sin T + 2x / 2) \u003d 0,
√2 Sin T / 2 Sin (π / 4 - T + 2x / 2) \u003d 0, prin urmare,
Sin T/2 = 0, apoi T = 2πk.
pentru că (х ± 2πk) є D f , unde f(x) = Sin x + Cos x,
f(х + t) = f(х), atunci funcția f(х) este periodică cu perioada cea mai mică pozitivă 2π.
Exemplul 2. Este funcția periodică f (x) \u003d Cos 2x Sin x, care este perioada ei?
Decizie. Fie f 1 (x) \u003d Cos 2x, apoi T 1 \u003d 2π: 2 \u003d π (vezi 2)
Fie f 2 (x) = Sin x, apoi T 2 = 2π. pentru că π/2π = ½ este un număr rațional, atunci această funcție este periodică. Perioada sa T = LCM
(π, 2π) = 2π.
Deci, această funcție este periodică cu o perioadă de 2π.
5. Fie funcția f(t), care nu este identic egală cu o constantă, continuă și periodică, atunci are cea mai mică perioadă pozitivă ω 0 , orice altă perioadă a lui ω are forma: ω= kω 0 , unde k є Z.
Notă: 1) Două condiții sunt foarte importante în această proprietate:
f(t) este continuă, f(t) ≠ C, unde C este o constantă.
2) Reversul nu este adevărat. Adică, dacă toate perioadele sunt comensurabile, atunci nu rezultă din aceasta că există cea mai mică perioadă pozitivă. Acestea. o funcție periodică poate să nu aibă cea mai mică perioadă pozitivă.
EXEMPLUL 1. f(t) = C, periodic. Perioada sa este orice număr real, nu există cea mai mică perioadă.
Exemplul 2. Funcția Dirichlet:
D(x) =
Orice număr rațional este perioada lui, nu există cea mai mică perioadă pozitivă.
6. Dacă f(t) este o funcție periodică continuă și ω 0 este cea mai mică perioadă pozitivă a acesteia, atunci funcția f(αt + β) are cea mai mică perioadă pozitivă ω 0 //α/. Această afirmație decurge din punctul 2.
Exemplul 1. Găsiți perioada funcției y \u003d Sin (2x - 5).
Decizie. y \u003d Sin (2x - 5) \u003d Sin (2 (x - 5/2)).
Graficul funcției y se obține din graficul funcției Sin x, mai întâi prin „comprimare” de două ori, apoi prin „deplasare” la dreapta cu 2,5. „Deplasarea nu afectează periodicitatea, T = π este perioada acestei funcții.
Este ușor să obțineți perioada acestei funcții folosind proprietatea articolului 6:
T \u003d 2π / 2 \u003d π.
7. Dacă f (t) - ω este o funcție periodică și are o derivată continuă f "(t), atunci f" (t) este, de asemenea, o funcție periodică, T \u003d ω
EXEMPLUL 1. f(t) = Sin t, T = 2πk. Derivata sa f "(t) = Cos t
F "(t) \u003d Cos t, T \u003d 2πk, k є Z.
EXEMPLUL 2. f(t) = Cos t, T = 2πk. Derivatul său
F "(t) \u003d - Sin t, T \u003d 2πk, k є Z.
Exemplul 3. f(t) =tg t, perioada sa este Т = πk.
F "(t) \u003d 1 / Cos 2 t este, de asemenea, periodic după elementul de proprietate 7 și are perioada T = πk. Cea mai mică perioadă pozitivă este T = π.
SARCINI.
№ 1
Este funcția f(t) = Sin t + Sin πt periodică?
Decizie. Pentru comparație, rezolvăm această problemă în două moduri.
În primul rând, prin definiția unei funcții periodice. Să presupunem că f(t) este periodic, atunci pentru orice t є D f avem:
Sin (t + T) + Sin π (t + T) = Sin t + Sin πt,
Sin (t + T) - Sin t \u003d Sin πt - Sin π (t + T),
2 Cos 2t + T/2 Sin T/2 = -2 Cos 2 πt + πt/2 Sin πt/2.
pentru că acest lucru este valabil pentru orice t є D f , atunci, în special, pentru t 0 , la care partea stângă a ultimei egalități dispare.
Atunci avem: 1) Cos 2t 0 + T/2 Sin T/2 = 0. Se rezolvă în raport cu T.
Sin Т/2 = 0 la Т = 2 πk, unde k є Z.
2) Cos 2πt 0 + πt 0 /2 Sin πТ/2 = 0. Rezolvați în raport cu Т.
Sin πТ/2 = 0, apoi Т = 2πn/ π = 2n, n≠0, unde n є Z.
pentru că avem o identitate, atunci 2 πk = 2n, π = 2n/2 k = n/ k, care nu poate fi, deoarece π este un număr irațional, iar n/k este rațional. Adică, presupunerea noastră că funcția f(t) este periodică nu a fost corectă.
În al doilea rând, soluția este mult mai simplă dacă folosim proprietățile de mai sus ale funcțiilor periodice:
Fie f 1 (t) = Sin t, Т 1 = 2 π; f 2 (t) = Sin πt, Т 2 - 2π/π = 2. Apoi, Т 1 /Т 2 = 2π/2 = π este un număr irațional, adică. perioadele T 1, T2 nu sunt proporționale, deci f(t) nu este periodică.
Raspuns: nu.
№ 2
Arătați că dacă α este un număr irațional, atunci funcția
F(t) = Cos t + Cos αt
nu este periodică.
Decizie. Fie f 1 (t) = Cos t, f 2 (t) = Cos αt.
Atunci perioadele lor sunt, respectiv, T 1 \u003d 2π, T 2 = 2π//α/ - cele mai mici perioade pozitive. Să găsim, T 1 /T 2 = 2π/α//2π = /α/ este un număr irațional. Deci T 1 și T 2 sunt incomensurabile, iar funcția
f(t) nu este periodic.
№ 3
Aflați cea mai mică perioadă pozitivă a funcției f(t) = Sin 5t.
Decizie. După elementul de proprietate 2 avem:
f(t) este periodic; T = 2π/5.
Răspuns: 2π/5.
№ 4
Este F(x) = arccos x + arcsin x o funcție periodică?
Decizie. Luați în considerare această funcție
F(x) \u003d arccos x + arcsin x \u003d π - arcsin x + arcsin x \u003d π,
acestea. F(x) este o funcție periodică (vezi elementul de proprietate 5, exemplul 1.).
Răspuns: da.
№ 5
Este o funcție periodică
F (x) \u003d Sin 2x + Cos 4x + 5?
decizie. Fie f 1 (x) = Sin 2x, apoi T 1 = π;
F 2 (x) \u003d Cos 4x, apoi T 2 \u003d 2π / 4 \u003d π / 2;
F 3 (x) \u003d 5, T 3 - orice număr real, în special T 3 putem presupune egal cu T 1 sau T 2 . Atunci perioada acestei funcții este T = LCM (π, π/2) = π. Adică f(x) este periodic cu perioada Т = π.
Răspuns: da.
№ 6
Este funcția f(x) = x - E(x) periodică, unde E(x) este o funcție care asociază argumentul x cu cel mai mic număr întreg care nu îl depășește pe cel dat.
Decizie. Adesea funcția f (x) se notează cu (x) - partea fracțională a numărului x, adică.
F(x) \u003d (x) \u003d x - E (x).
Fie f(х) o funcție periodică, adică. există un număr T >0 astfel încât x - E(x) = x + T - E(x + T). Să scriem această ecuație
(x) + E(x) - E(x) = (x + T) + E(x + T) - E(x + T),
(x) + (x + T) - adevărat pentru orice x din domeniul D f, cu condiția ca T ≠ 0 și T є Z. Cel mai mic pozitiv dintre ele este T = 1, adică. T = 1 astfel încât
X + T - E (x + T) \u003d x - E (x),
În plus, (х ± Тk) є D f, unde k є Z.
Răspuns: Această funcție este periodică.
№ 7
Este funcția f(x) = Sin x periodică? 2 .
Decizie. Să spunem f(x) = Sin x 2 functie periodica. Atunci, prin definiția unei funcții periodice, există un număr T ≠ 0 astfel încât: Sin x 2 \u003d Sin (x + T) 2 pentru orice x є D f.
Sin x 2 \u003d Sin (x + T) 2 \u003d 0,
2 Cos x 2 + (x + T) 2 / 2 Sin x 2 - (x + T) 2 / 2 \u003d 0, atunci
Cos x 2 + (x + T) 2 / 2 = 0 sau Sin x 2 - (x + T) 2 / 2 = 0.
Luați în considerare prima ecuație:
Cos x 2 + (x + T) 2 / 2 \u003d 0,
X 2 + (x + T) 2 / 2 \u003d π (1 + 2 k) / 2 (k є Z),
T \u003d √ π (1 + 2 k) - x 2 - x. (unu)
Luați în considerare a doua ecuație:
Sin x 2 - (x + T) 2 / 2 \u003d 0,
X + T \u003d √- 2πk + x 2,
T \u003d √x 2 - 2πk - x. (2)
Din expresiile (1) și (2) se poate observa că valorile găsite ale lui T depind de x, adică. nu există T>0 astfel încât
Sin x 2 \u003d Sin (x + T) 2
Pentru orice x din domeniul acestei funcții. f(x) nu este periodic.
Raspuns: nu
№ 8
Investigați periodicitatea funcției f(x) = Cos 2 x.
Decizie. Să reprezentăm f(x) prin formula cosinusului cu unghi dublu
F(x) = 1/2 + 1/2 Cos 2x.
Fie f 1 (x) = ½, apoi T 1 - poate fi orice număr real; f 2 (x) \u003d ½ Cos 2x este o funcție periodică, deoarece produsul a două funcții periodice având o perioadă comună T 2 = pi. Apoi, cea mai mică perioadă pozitivă a acestei funcții
T \u003d LCM (T 1, T 2) \u003d π.
Deci, funcția f(x) = Cos 2 x – π – este periodic.
Răspuns: π este periodic.
№ 9
Poate fi domeniul unei funcții periodice:
A) semi-linia [a, ∞),
B) tăiat?
Decizie. Nu, pentru că
A) prin definiția unei funcții periodice, dacă х є D f, atunci și x ± ω
Trebuie să aparțină domeniului de aplicare al funcției. Fie x = a, atunci
X 1 \u003d (a - ω) є [a, ∞);
B) fie x = 1, apoi x 1 \u003d (1 + T) є.
№ 10
Poate fi o funcție periodică:
A) strict monoton;
B) par;
B) nici măcar?
Decizie. a) Fie f(x) o funcție periodică, i.e. există T≠0 astfel încât pentru orice x din domeniul funcțiilor D f ce e
(x ± T) є D f și f (x ± T) \u003d f (x).
Remediați orice x 0 º D f , deoarece f(x) este periodic, atunci (x 0 + T) є D f și f (x 0) \u003d f (x 0 + T).
Să presupunem că f(x) este strict monoton și pe întregul domeniu al definiției D f , de exemplu, crește. Apoi, prin definiția unei funcții crescătoare pentru orice x 1 și x 2 din domeniul D f din inegalitatea x 1 2 rezultă că f(x 1 ) 2 ). În special, din condiția x 0 0 + T, rezultă că
F(x 0 ) 0 +T), care contrazice condiția.
Aceasta înseamnă că o funcție periodică nu poate fi strict monotonă.
b) Da, o funcție periodică poate fi pară. Să luăm câteva exemple.
F (x) \u003d Cos x, Cos x \u003d Cos (-x), T \u003d 2π, f (x) este o funcție periodică pară.
0 dacă x este un număr rațional;
D(x) =
1 dacă x este un număr irațional.
D(x) = D(-x), domeniul funcției D(x) este simetric.
Funcția Direchlet D(x) este o funcție periodică pară.
f(x) = (x),
f (-x) \u003d -x - E (-x) \u003d (-x) ≠ (x).
Această funcție nu este chiar.
c) O funcție periodică poate fi impară.
f (x) \u003d Sin x, f (-x) \u003d Sin (-x) \u003d - Sin \u003d - f (x)
f(x) este o funcție periodică impară.
f (x) - Sin x Cos x, f (-x) \u003d Sin (-x) Cos (-x) \u003d - Sin x Cos x \u003d - f (x),
f(x) este impar și periodic.
f(x) = ℓ Sin x, f(-x) = ℓ Sin(- x) = ℓ -Sin x ≠ - f(x),
f(x) nu este impar.
f(х) = tg x este o funcție periodică impară.
Răspuns: nu; Da; Da.
№ 11
Câte zerouri poate avea o funcție periodică pe:
unu) ; 2) pe toată axa reală, dacă perioada funcției este egală cu T?
Rezolvare: 1. a) Pe intervalul [a, b], o funcție periodică poate să nu aibă zerouri, de exemplu, f(x) = C, C≠0; f (x) \u003d Cos x + 2.
b) Pe intervalul [a, b], o funcție periodică poate avea un număr infinit de zerouri, de exemplu, funcția Direchlet
0 dacă x este un număr rațional,
D(x) =
1 dacă x este un număr irațional.
c) Pe segmentul [a, b], o funcție periodică poate avea un număr finit de zerouri. Să găsim acest număr.
Fie T perioada funcției. Denota
X 0 = (min x є(a,b), astfel încât f(х) = 0).
Apoi numărul de zerouri de pe segmentul [a, b]: N = 1 + E (în x 0 /T).
Exemplul 1. x є [-2, 7π / 2], f (x) \u003d Cos 2 х este o funcție periodică cu perioada Т = π; X 0 = -π/2; apoi numărul de zerouri al funcției f(x) pe intervalul dat
N \u003d 1 + E (7π / 2 - (-π / 2) / 2) \u003d 1 + E (8π / 2π) \u003d 5.
Exemplul 2. f (x) \u003d x - E (x), x є [-2; 8.5]. f(х) – funcție periodică, Т + 1,
x 0 = -2. Apoi numărul de zerouri al funcției f(x) pe segmentul dat
N \u003d 1 + E (8,5 - (-2) / 1) \u003d 1 + E (10,5 / 1) \u003d 1 + 10 \u003d 11.
Exemplul 3. f (x) \u003d Cos x, x є [-3π; π], T 0 \u003d 2π, x 0 \u003d - 5π / 2.
Apoi numărul de zerouri ale acestei funcții pe un segment dat
N \u003d 1 + E (π - (-5π / 2) / 2π) \u003d 1 + E (7π / 2π) \u003d 1 + 3 \u003d 4.
2. a) Un număr infinit de zerouri, deoarece X 0 є D f și f(х 0 ) = 0, atunci pentru toate numerele
X 0 + Tk, unde k є Z, f (x 0 ± Tk) = f (x 0 ) =0, iar punctele de forma x 0 ± Tk este o mulțime infinită;
b) nu au zerouri; dacă f(х) este periodică și pentru oricare
х є D f funcția f(x) >0 sau f(x)
F(x) \u003d Sin x +3,6; f(x) = C, C ≠ 0;
F(x) \u003d Sin x - 8 + Cos x;
F(x) = Sin x Cos x + 5.
№ 12
Poate fi periodică suma funcțiilor neperiodice?
Decizie. Da poate. De exemplu:
- f1 (х) = х este neperiodic, f 2 (x) \u003d E (x) - neperiodic
F (x) \u003d f 1 (x) - f 2 (x) \u003d x - E (x) - periodic.
- f1 (x) \u003d x - neperiodic, f (x) \u003d Sin x + x - neperiodic
F (x) \u003d f 2 (x) - f 1 (x) = Sin x - periodic.
Răspuns: da.
№ 13
Funcția f(x) și φ(x) sunt periodice cu perioade T 1 și T 2 respectiv. Produsul lor este întotdeauna o funcție periodică?
Decizie. Nu, doar dacă T 1 și T 2 - comparabil. De exemplu,
F(x) \u003d Sin x Sin πx, T 1 \u003d 2π, T 2 \u003d 2; apoi T 1 /T 2 = 2π/2 = π este un număr irațional, deci f(х) nu este periodic.
f (x) \u003d (x) Cos x \u003d (x - E (x)) Cos x. Fie f 1 (x) \u003d x - E (x), T 1 \u003d 1;
f 2 (x) \u003d Cos (x), T 2 \u003d 2π. T2/T1 = 2π/1 = 2π, deci f(x) nu este periodic.
Răspuns: Nu.
Sarcini pentru soluție independentă
Care dintre funcții sunt periodice, găsiți perioada?
1. f (x) \u003d Sin 2x, 10. f (x) \u003d Sin x / 2 + tg x,
2. f (x) \u003d Cos x / 2, 11. f (x) \u003d Sin 3x + Cos 4x,
3. f (x) \u003d tg 3x, 12. f (x) \u003d Sin 2 x+1,
4. f(x) = Cos (1 - 2x), 13. f(x) = tg x + ctg√2x,
5. f (x) \u003d Sin x Cos x, 14. f (x) \u003d Sin πx + Cos x,
6. f (x) \u003d ctg x / 3, 15. f (x) \u003d x 2 - E (x 2),
7. f (x) \u003d Sin (3x - π / 4), 16. f (x) \u003d (x - E (x)) 2 ,
8. f (x) \u003d Sin 4 x + Cos 4 x, 17. f (x) \u003d 2 x - E (x),
9. f(x) = Sin 2 x, 18. f(x) = x – n + 1 dacă n ≤ x≤ n + 1, n = 0, 1, 2…
№ 14
Fie f(x) - T o funcție periodică. Care dintre funcții sunt periodice (găsiți T)?
- φ(x) = f(x + λ) este periodic, deoarece „deplasarea” de-a lungul axei Ox nu afectează ω; perioada sa ω = T.
- φ(х) = а f(х + λ) + в este o funcție periodică cu perioada ω = Т.
- φ(x) = f(kx) este o funcție periodică cu perioada ω = T/k.
- φ(x) \u003d f (ax + b) - o funcție periodică cu o perioadă ω \u003d T / a.
- φ(x) = f(√x) nu este periodic, deoarece domeniul său de definiție Dφ = (x/x ≥ 0), în timp ce domeniul de definire al unei funcții periodice nu poate fi o semiaxă.
- φ(x) = (f(x) + 1/(f(x) - 1) este o funcție periodică, deoarece
φ (x + T) \u003d f (x + T) + 1 / f (x + T) - 1 \u003d φ (x), ω \u003d T.
- φ (x) \u003d a f 2 (x) + în f (x) + c.
Fie φ 1 (x) = a f 2 (x) - periodic, ω 1 = t/2;
φ 2 (х) = în f(х) – periodic, ω 2=T/T=T;
φ 3 (х) = с – periodic, ω 3 - orice număr;
atunci ω = LCM(Т/2; Т) = Т, φ(х) este periodic.
Altfel, pentru că domeniul acestei funcții este întreaga linie numerică, apoi setul de valori ale funcției f - E f є D φ , deci funcția
φ(х) este periodic și ω = Т.
- φ(х) = √φ(х), f(х) ≥ 0.
φ(х) este periodic cu perioada ω = Т, deoarece pentru orice x, funcția f(x) ia valorile f(x) ≥ 0, adică. setul său de valori E f є D φ , unde
Dφ este domeniul de definire al funcției φ(z) = √z.
№ 15
Este funcția f(x) = x 2 periodice?
Decizie. Se consideră x ≥ 0, atunci pentru f(x) există o funcție inversă √x, ceea ce înseamnă că pe acest interval f(x) este o funcție monotonă, atunci nu poate fi periodică (vezi Nr. 10).
№ 16
Dat un polinom P(x) = a 0 + a 1 x + a 2 x + ... a n x.
Este P(x) o funcție periodică?
Decizie. 1. Dacă identitatea este constantă, atunci P(x) este o funcție periodică, adică. în cazul în care un i = 0, unde i ≥ 1.
2. Fie P(x) ≠ c, unde c este o constantă. Fie P(x) o funcție periodică, iar P(x) are rădăcini reale, atunci din moment ce P(x) este o funcție periodică, atunci trebuie să existe un număr infinit de ele. Și conform teoremei fundamentale a algebrei, numărul lor k este astfel încât k ≤ n. Deci P(x) nu este o funcție periodică.
3. Fie P(x) un polinom care este identic diferit de zero și nu are rădăcini reale. Să presupunem că P(x) este o funcție periodică. Introducem polinomul q(x) = a 0 , q(х) este o funcție periodică. Se consideră diferența P(x) - q(x) = a 1 x 2 + ... + a n x n.
pentru că există o funcție periodică în partea stângă a egalității, apoi funcția din partea dreaptă este, de asemenea, periodică, în plus, are cel puțin o rădăcină reală, x \u003d 0. Dacă funcția este periodică, atunci trebuie să existe un număr infinit de zerouri. Avem o contradicție.
P(x) nu este o funcție periodică.
№ 17
Funcția f(t) – T este periodică. Este funcția f la (t), unde
k є Z, o funcție periodică, cum sunt legate perioadele lor?
Decizie. Demonstrarea se va realiza prin metoda funcției matematice. Lasa
f 1 = f(t), atunci f 2 = f 2 (t) = f(t) f(t),
F 3 \u003d f 3 (t) \u003d f (t) f 2 este o funcție periodică conform proprietății articolului 4.
………………………………………………………………………….
Fie f k-1 = f k-1 (t) este o funcție periodică și perioada sa Т k-1 proporțional cu perioada T. Înmulțim ambele părți ale ultimei egalități cu f(t), obținem f k-1 f(t) = f(t) f k-1 (t),
F la = f la (t) este o funcție periodică după elementul de proprietate 4. ω ≤ Т.
№ 18
Fie f(x) o funcție arbitrară definită pe . Este funcția f((x)) periodică?
A n e t: da, pentru că setul de valori ale funcției (x) aparține domeniului de definire a funcției f(x), apoi, după elementul de proprietate 3, f((x)) este o funcție periodică, perioada sa ω = T = 1.
№ 19
F(x) este o funcție arbitrară definită pe [-1; 1], funcția f(sinx) este periodică?
Răspuns: da, perioada sa este ω = T = 2π (dovada este similară cu #18).
În sarcinile școlare normale dovedi periodicitatea cutare sau cutare funcție nu este de obicei dificilă: astfel, pentru a verifica dacă funcția $y=sin\frac34 x+sin\frac27 x$ este periodică, este suficient să rețineți că produsul $T=4\times7\times 2 \pi$ este perioada sa: dacă adăugăm numărul T la x, atunci acest produs va „mânca” ambii numitori și sub semnul sinus vor fi de prisos numai multipli întregi de $2\pi$, pe care sinusul însuși îi va „mânca” .
Dar dovada neperiodicitatii una sau alta funcție direct prin definiție poate să nu fie deloc simplă. Deci, pentru a demonstra neperiodicitatea funcției $y=\sin x^2$ considerată mai sus, se poate scrie egalitatea $sin(x+T)^2=\sin x^2$, dar nu o rezolvați din obişnuinţă ecuație trigonometrică, și ghiciți să înlocuiți x=0 în el, după care restul se va dovedi aproape automat: $\sin T^2=0$, $T^2=k\pi$, unde k este un număr întreg mai mare decât 0, adică . $T=\sqrt (k\pi)$, iar dacă acum ghiciți și înlocuiți $x=\sqrt (\pi)$ în el, se dovedește că $\sin(\sqrt(\pi)+\sqrt( k\ pi))=0$, de unde $\sqrt(\pi)+\sqrt(k\pi)=n\pi$, $1+\sqrt(k)=n\sqrt(\pi)$, $1+ k+ 2\sqrt(k)=n^2\pi$, $2\sqrt(k)=n^2\pi-1-k=n^2\pi=m$, $4k=n^4(\pi ) ^2+2mn^2x+m^2$, și astfel p este rădăcina ecuației $n^4x^2+2mn^2\pi+m^2-4k=0$, adică. este algebrică, ceea ce nu este adevărat: $\pi$ este, după cum știm, transcendental, adică. nu este o rădăcină a vreunei ecuații algebrice cu coeficienți întregi. Cu toate acestea, în viitor vom obține o dovadă mult mai simplă a acestei afirmații - dar cu ajutorul instrumentelor de analiză matematică.
Când se demonstrează neperiodicitatea funcțiilor, un truc logic elementar ajută adesea: dacă toate funcțiile periodice au o anumită proprietate, dar această funcție nu o are, atunci, desigur, nu este periodică. Astfel, o funcție periodică ia oricare dintre valorile sale de nenumărate ori și, prin urmare, de exemplu, funcția $y=\frac(3x^2-5x+7)(4x^3-x+2)$ este nu periodic, deoarece valoarea 7 este nevoie de doar două puncte. Adesea, pentru a demonstra neperiodicitatea, este convenabil să folosiți singularitățile sale domenii, iar pentru a găsi proprietatea dorită a funcțiilor periodice, uneori trebuie să arăți o anumită imaginație.
De asemenea, observăm că de foarte multe ori întrebarea, ce este o funcție non-periodică, trebuie să auziți un răspuns în stilul despre care am vorbit în legătură cu funcții pare și impare, este atunci când $f(x+T)\neq f(x)$, ceea ce, desigur, nu este permis.
Și răspunsul corect depinde de definiția specifică a unei funcții periodice și, pe baza definiției date mai sus, se poate spune, desigur, că o funcție este neperiodică dacă nu are o singură perioadă, dar aceasta va fi o definiție „rea” care nu dă direcție dovezi de non-periodicitate. Și dacă o descifrăm mai departe, descriind ce înseamnă propoziția „funcția f nu are punct” sau, ceea ce este același lucru, „nici un număr $T \neq 0$ nu este o perioadă a funcției f”, atunci obținem că funcția f nu este periodică dacă și numai dacă pentru fiecare $T \neq 0$ există un număr $x\în D(f)$ astfel încât fie cel puțin unul dintre numerele $x+T$ și $x-T$ este nu aparține lui D(f), sau $f(x+T)\neq f(x)$.
Se poate spune și altfel: „Există un număr $x\în D(f)$ astfel încât egalitatea $f(x+T) = f(x)$ nu este valabilă” - această egalitate poate să nu fie valabilă pentru doi motive: fie ea nu are sens, adică una dintre părțile sale nu este definită sau, în caz contrar, nu este validă. De dragul interesului, adăugăm că efectul de limbaj despre care am vorbit mai sus se manifestă și aici: pentru egalitate, „a nu fi adevărat” și „a greși” nu sunt același lucru - egalitatea poate să nu aibă sens.
O clarificare detaliată a cauzelor și consecințelor acestui efect lingvistic nu este, de fapt, subiectul matematicii, ci teoria limbajului, lingvistica sau, mai degrabă, secțiunea sa specială: semantica - știința sensului, unde, totuși, aceste întrebări sunt foarte complexe și nu au o soluție clară. Iar matematica, inclusiv matematica școlară, este nevoită să suporte aceste dificultăți și să depășească „tulburările” lingvistice – atâta timp cât și în măsura în care folosește, alături de limbajul simbolic, natural.
Scop: generalizarea și sistematizarea cunoștințelor elevilor pe tema „Periodicitatea funcțiilor”; să formeze abilități în aplicarea proprietăților unei funcții periodice, găsirea celei mai mici perioade pozitive a unei funcții, trasarea funcțiilor periodice; promovarea interesului pentru studiul matematicii; cultivați observația, acuratețea.
Echipamente: computer, proiector multimedia, carduri de sarcini, diapozitive, ceasuri, mese ornamentale, elemente de meșteșuguri populare
„Matematica este ceea ce oamenii folosesc pentru a controla natura și pe ei înșiși”
UN. Kolmogorov
În timpul orelor
I. Etapa organizatorică.
Verificarea gradului de pregătire a elevilor pentru lecție. Prezentarea temei și a obiectivelor lecției.
II. Verificarea temelor.
Verificăm temele în funcție de mostre, discutăm cele mai dificile puncte.
III. Generalizarea și sistematizarea cunoștințelor.
1. Lucru frontal oral.
Întrebări de teorie.
1) Formați definiția perioadei funcției
2) Care este cea mai mică perioadă pozitivă a funcțiilor y=sin(x), y=cos(x)
3). Care este cea mai mică perioadă pozitivă a funcțiilor y=tg(x), y=ctg(x)
4) Folosiți cercul pentru a demonstra corectitudinea relațiilor:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n ∈ Z
ctg(x+π n)=ctgx, n ∈ Z

sin(x+2π n)=sinx, n ∈ Z
cos(x+2π n)=cosx, n ∈ Z
5) Cum se trasează o funcție periodică?
exerciții orale.
1) Demonstrați următoarele relații
A) sin(740º) = sin(20º)
b) cos(54º ) = cos(-1026º)
c) sin(-1000º) = sin(80º )
2. Demonstrați că unghiul de 540º este una dintre perioadele funcției y= cos(2x)
3. Demonstrați că unghiul de 360º este una dintre perioadele funcției y=tg(x)
4. Transformați aceste expresii astfel încât unghiurile incluse în ele să nu depășească 90º în valoare absolută.
A) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)
5. Unde te-ai întâlnit cu cuvintele PERIOADĂ, PERIODICITATE?
Răspunsurile elevilor: O perioadă în muzică este o construcție în care este enunțată o gândire muzicală mai mult sau mai puțin completă. Perioada geologică face parte dintr-o eră și este împărțită în epoci cu o perioadă cuprinsă între 35 și 90 de milioane de ani.
Timpul de înjumătățire al unei substanțe radioactive. Fracție periodică. Periodicele sunt publicații tipărite care apar la date strict definite. Sistem periodic Mendeleev.
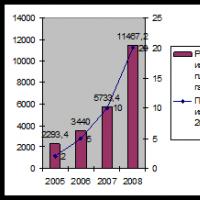
6. Figurile prezintă părți din graficele funcțiilor periodice. Definiți perioada funcției. Determinați perioada funcției.

Răspuns: T=2; T=2; T=4; T=8.
7. Unde în viața ta te-ai întâlnit cu construcția de elemente care se repetă?
Elevii răspund: Elemente de ornamente, artă populară.

IV. Rezolvarea colectivă a problemelor.
(Rezolvarea problemelor pe diapozitive.)
Să luăm în considerare una dintre modalitățile de a studia o funcție pentru periodicitate.
Această metodă ocolește dificultățile asociate cu demonstrarea că una sau alta perioadă este cea mai mică și, de asemenea, nu este nevoie să abordăm întrebări despre operațiile aritmetice asupra funcțiilor periodice și despre periodicitatea unei funcții complexe. Raționamentul se bazează doar pe definiția unei funcții periodice și pe următorul fapt: dacă T este perioada funcției, atunci nT(n? 0) este perioada acesteia.
Problema 1. Aflați cea mai mică perioadă pozitivă a funcției f(x)=1+3(x+q>5)
Soluție: Să presupunem că perioada T a acestei funcții. Atunci f(x+T)=f(x) pentru toate x ∈ D(f), adică.
1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)
Fie x=-0,25 obținem
(T)=0<=>T=n, n ∈ Z
Am obținut că toate perioadele funcției considerate (dacă există) sunt între numere întregi. Alegeți dintre aceste numere cel mai mic număr pozitiv. Aceasta este 1 . Să verificăm dacă este de fapt o perioadă 1 .
f(x+1)=3(x+1+0,25)+1
Deoarece (T+1)=(T) pentru orice T, atunci f(x+1)=3((x+0.25)+1)+1=3(x+0.25)+1=f(x ), adică. 1 - perioada f. Deoarece 1 este cel mai mic dintre toate numerele întregi pozitive, atunci T=1.
Sarcina 2. Arătați că funcția f(x)=cos 2 (x) este periodică și găsiți perioada ei principală.

Sarcina 3. Găsiți perioada principală a funcției
f(x)=sin(1,5x)+5cos(0,75x)
Presupuneți perioada T a funcției, apoi pentru oricare X raportul
sin1.5(x+T)+5cos0.75(x+T)=sin(1.5x)+5cos(0.75x)
Dacă x=0 atunci
sin(1.5T)+5cos(0.75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Dacă x=-T, atunci
sin0+5cos0=sin(-1.5T)+5cos0.75(-T)
5= - sin(1.5T)+5cos(0.75T)
| sin(1,5T)+5cos(0,75T)=5 – sin(1,5Т)+5cos(0,75Т)=5 |
Adăugând, obținem:
10cos(0,75T)=10
2π n, n € Z
Să alegem dintre toate numerele „suspecte” pentru perioada cea mai mică pozitivă și să verificăm dacă este o perioadă pentru f. Acest număr
f(x+)=sin(1.5x+4π)+5cos(0.75x+2π)= sin(1.5x)+5cos(0.75x)=f(x)
Prin urmare, este perioada principală a funcției f.
Sarcina 4. Verificați dacă funcția f(x)=sin(x) este periodică
Fie T perioada funcției f. Apoi pentru orice x
sin|x+T|=sin|x|
Dacă x=0, atunci sin|T|=sin0, sin|T|=0 T=π n, n ∈ Z.
Presupune. Că pentru unele n numărul π n este o perioadă
funcția considerată π n>0. Atunci sin|π n+x|=sin|x|

Acest lucru implică faptul că n trebuie să fie și par și impar în același timp, ceea ce este imposibil. Prin urmare, această funcție nu este periodică.
Sarcina 5. Verificați dacă funcția este periodică
f(x)= 
Fie T perioada f, atunci
 , deci sinT=0, T=π n, n € Z. Să presupunem că pentru unele n numărul π n este într-adevăr perioada funcției date. Atunci numărul 2π n va fi și o perioadă
, deci sinT=0, T=π n, n € Z. Să presupunem că pentru unele n numărul π n este într-adevăr perioada funcției date. Atunci numărul 2π n va fi și o perioadă

Deoarece numărătorii sunt egali, la fel și numitorii lor, deci

Prin urmare, funcția f nu este periodică.
Lucru de grup.
Sarcini pentru grupa 1.
Sarcini pentru grupa 2.
Verificați dacă funcția f este periodică și găsiți perioada ei principală (dacă există).
f(x)=cos(2x)+2sin(2x)
Sarcini pentru grupa 3.
La finalul lucrării, grupurile își prezintă soluțiile.
VI. Rezumând lecția.
Reflecţie.
Profesorul dă elevilor cartonașe cu desene și se oferă să picteze peste o parte a primului desen în funcție de măsura în care, după cum li se pare, ei au stăpânit metodele de studiere a funcției pentru periodicitate și, în parte, a celui de-al doilea desen. , în conformitate cu contribuția lor la lucrarea din lecție.
VII. Teme pentru acasă
unu). Verificați dacă funcția f este periodică și găsiți perioada ei principală (dacă există)
b). f(x)=x 2 -2x+4
c). f(x)=2tg(3x+5)
2). Funcția y=f(x) are o perioadă T=2 și f(x)=x 2 +2x pentru x € [-2; 0]. Aflați valoarea expresiei -2f(-3)-4f(3,5)
Literatură/
- Mordkovich A.G. Algebra și începutul analizei cu studiu aprofundat.
- Matematică. Pregătirea pentru examen. Ed. Lysenko F.F., Kulabukhova S.Yu.
- Sheremetyeva T.G. , Tarasova E.A. Algebră și analiză de început pentru clasele 10-11.
Caracteristici ale trasării funcțiilor periodice
Graficul unei funcții periodice este de obicei construit mai întâi pe intervalul [ X 0 ; X 0 + T). Se efectuează transferul paralel al punctelor graficului către întreaga zonă de definire.
Exemple de funcții periodice și graficele acestora.
Funcțiile trigonometrice pot servi ca exemple de funcții periodice. Să le luăm în considerare pe cele principale.
Funcția F(x)=sin(x)
a) Domeniul de definire: D (sin x) = R .
b) Mulțimea valorilor: E (sin x) = [– 1 , 1] .
c) Par, impar: funcția este impar.
d) Periodicitate: funcția este periodică cu perioada principală .
e) Zerurile funcției: sin x = 0 pentru , n Z.
f) Intervale de constanță a funcției:
g) Intervale de monotonitate: funcţia creşte la ;
funcția scade atunci când,
h) Funcția extremă:
; .
Graficul funcției y= sin x este prezentat în figură.
Funcția F(x) = cos(x)
a) Domeniul de definire.
b) Setul de valori: E (cos X) = [ – 1 , 1 ] .
c) Par, impar: funcția este pară.
G ) Periodicitate: Funcția este periodică cu o perioadă de bază de .
e) Zerourile funcţiei: la .
f) Intervale de constanță a semnului:
g) Intervale de monotonitate:
functia creste la ;
functia scade cand
h) Extreme:
Graficul funcției y= cos X prezentată în figură.
Funcția F(x) = tg(x)
a) Domeniul de aplicare:
b) Set de valori: E ()
c) Par, impar. Funcția este ciudată.
d) Periodicitatea. Functie periodica cu perioada principala
e) Zerourile funcției: tg x = 0 pentru x = n, n Z.
f) Intervale de constanță a semnelor:
g) Intervale de monotonitate: funcția crește pe fiecare interval care aparține în întregime domeniului său de definiție.
h) Extreme: niciuna.
Graficul funcției y=tg X prezentată în figură.
Funcția F(x) = ctg(x)
a) Domeniul de definire: D (ctg x) = R\ (n(n Z)).
b) Multime de valori: E (ctg x) = R .
c) Par, funcția impară este impară.
d) Periodicitate: funcţia este periodică cu perioada principală T = .
e) Zerourile funcției: ctg x = 0 pentru x = /2 + n, n Z.
f) Intervale de constanţă a semnului;
g) Intervale de monotonitate: funcția scade pe fiecare interval care aparține în întregime domeniului său de definiție.
h) Extreme: niciuna.
Graficul funcției y = ctg x este prezentat în figură.
Grafice interesante se obțin folosind suprapunerea - formarea de funcții complexe bazate pe funcții periodice trigonometrice.
Graficul unei funcții periodice
II. Aplicații ale funcțiilor periodice. fluctuatii periodice.
Fluctuații.
fluctuatii se numesc procese care diferă în diferite grade de repetare. Oscilațiile sunt procese care se repetă la intervale regulate (cu toate acestea, nu toate procesele care se repetă sunt oscilații). În funcție de natura fizică a procesului repetat, se disting oscilații mecanice, electromagnetice, electromecanice etc. La vibratii mecanice poziţiile şi coordonatele corpurilor se modifică periodic. Cu electrice - tensiune și curent. În funcție de natura impactului asupra unui sistem oscilant, se disting oscilații libere, oscilații forțate, autooscilații și oscilații parametrice.
recurente procesele au loc continuu în interiorul oricărui organism viu, de exemplu: contracțiile inimii, funcția pulmonară; tremurăm când ne este frig; auzim și vorbim datorită vibrațiilor timpanelor și a corzilor vocale; Când mergem, picioarele noastre fac mișcări oscilatorii. Atomii care ne fac să vibrăm. Lumea în care trăim este predispusă la fluctuații.
fluctuatii periodice.
periodic numite astfel de oscilații în care toate caracteristicile mișcării se repetă după o anumită perioadă de timp.
Pentru oscilațiile periodice se folosesc următoarele caracteristici:
perioada de oscilatie T, egal cu timpul în care are loc o oscilație completă;
frecvența de oscilațieν, egal cu numărul de oscilații pe secundă (ν = 1/T);
Oscilațiile parametrice sunt efectuate cu o modificare periodică a parametrilor unui sistem oscilant (o persoană care se balansează într-un leagăn își ridică și coboară periodic centrul de greutate, modificând astfel parametrii sistemului). În anumite condiții, sistemul devine instabil - o abatere aleatorie de la poziția de echilibru duce la apariția și creșterea oscilațiilor. Acest fenomen se numește excitație parametrică a oscilațiilor (adică, oscilațiile sunt excitate prin modificarea parametrilor sistemului), iar oscilațiile în sine sunt numite parametrice. În ciuda diferitelor natura fizica, oscilațiile sunt caracterizate de aceleași regularități care sunt studiate metode comune. O caracteristică cinematică importantă este forma vibrațiilor. Este determinată de forma funcției timpului, care descrie modificarea uneia sau alteia mărimi fizice în timpul oscilațiilor. Cele mai importante sunt astfel de fluctuații în care valoarea fluctuantă se modifică în timp conform legii sinusului sau cosinusului. Se numesc armonici. Acest tip de oscilație este deosebit de important din următoarele motive. În primul rând, oscilațiile în natură și tehnologie au adesea un caracter foarte apropiat de armonic. În al doilea rând, procesele periodice de o formă diferită (cu o dependență diferită de timp) pot fi reprezentate ca o suprapunere, sau suprapunere, a oscilațiilor armonice.
Repetarea valorilor sale la un interval regulat al argumentului, adică neschimbarea valorii sale atunci când un număr fix diferit de zero este adăugat la argument ( perioadă funcții) pe întregul domeniu de definire.
Mai formal, se spune că funcția este periodică cu punct T ≠ 0 (\displaystyle T\neq 0), dacă pentru fiecare punct x (\displaystyle x) din zona sa de definire a punctului x + T (\displaystyle x+T)și x − T (\displaystyle x-T) de asemenea, aparțin domeniului său de definiție, iar pentru ei egalitatea f (x) = f (x + T) = f (x - T) (\displaystyle f(x)=f(x+T)=f(x-T)).
Pe baza definiției, egalitatea este valabilă și pentru o funcție periodică f (x) = f (x + n T) (\displaystyle f(x)=f(x+nT)), Unde n (\displaystyle n)- orice număr întreg.
Cu toate acestea, dacă un set de perioade ( T , T > 0 , T ∈ R ) (\displaystyle \(T,T>0,T\in \mathbb (R) \)) există o valoare cea mai mică, se numește perioada principală (sau principală). funcții.
Exemple
Sin (x + 2 π) = sin x , cos (x + 2 π) = cos x , ∀ x ∈ R . (\displaystyle \sin(x+2\pi)=\sin x,\;\cos(x+2\pi)=\cos x,\quad \forall x\in \mathbb (R) .)
- Funcția Dirichlet este periodică; perioada sa este orice număr rațional diferit de zero. De asemenea, nu are o perioadă principală.
Câteva caracteristici ale funcțiilor periodice
și T 2 (\displaystyle T_(2))(Cu toate acestea, acest număr va fi pur și simplu o perioadă). De exemplu, funcția f (x) = sin (2 x) − sin (3 x) (\displaystyle f(x)=\sin(2x)-\sin(3x)) perioada principală este 2 π (\displaystyle 2\pi ), la functie g (x) = sin (3 x) (\displaystyle g(x)=\sin(3x)) perioada este 2 π / 3 (\displaystyle 2\pi /3), și suma lor f (x) + g (x) = sin (2 x) (\displaystyle f(x)+g(x)=\sin(2x)) perioada principală este evident egală cu π (\displaystyle \pi ).- Suma a două funcții cu perioade incomensurabile nu este întotdeauna o funcție neperiodică.