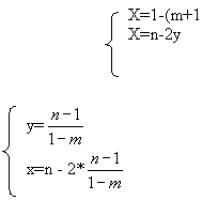Ţintă:

• Rezolvarea repetă a sistemelor de ecuații liniare cu două variabile
• definiți un sistem de ecuații liniare cu parametri
• vă va învăța cum să rezolvați sisteme de ecuații liniare cu parametri.

În timpul orelor

1. Organizarea timpului
2. Repetiţie
3. Explicarea unui subiect nou
4. Consolidare
5. Rezumatul lecției
6. Teme pentru acasă

2. Repetiție:

I. Ecuație liniară cu o variabilă:

1. Definiți o ecuație liniară cu o variabilă

[O ecuație de forma ax=b, unde x este o variabilă, a și b sunt niște numere, se numește ecuație liniară cu o variabilă]

2. Câte rădăcini poate avea o ecuație liniară?

[- Dacă a=0, b0, atunci ecuația nu are soluții, x

Dacă a=0, b=0, atunci x R

Dacă a0, atunci ecuația are o soluție unică, x =

3. Aflați câte rădăcini are ecuația (în funcție de opțiuni)

II. Ecuație liniară cu 2 variabile și sistem de ecuații liniare cu 2 variabile.

1. Definiți o ecuație liniară în două variabile. Dă un exemplu.

[O ecuație liniară cu două variabile este o ecuație de forma ax + by = c, unde x și y sunt variabile, a, b și c sunt niște numere. De exemplu, x-y=5]

2. Cum se numește rezolvarea unei ecuații cu două variabile?

[O soluție la o ecuație cu două variabile este o pereche de valori de variabile care transformă ecuația într-o egalitate adevărată.]

3. Este perechea de valori a variabilelor x = 7, y = 3 o soluție a ecuației 2x + y = 17?

4. Cum se numește graficul unei ecuații în două variabile?

[Graficul unei ecuații cu două variabile este mulțimea tuturor punctelor de pe planul de coordonate ale căror coordonate sunt soluții ale acestei ecuații.]

5. Aflați care este graficul ecuației:

[Să exprimăm variabila y prin x: y=-1,5x+3

Formula y=-1,5x+3 este o funcție liniară, al cărei grafic este o linie dreaptă. Deoarece ecuațiile 3x+2y=6 și y=-1,5x+3 sunt echivalente, această dreaptă este, de asemenea, un grafic al ecuației 3x+2y=6]

6. Care este graficul ecuației ax+bу=c cu variabilele x și y, unde a0 sau b0?

[Graficul unei ecuații liniare cu două variabile în care cel puțin unul dintre coeficienții variabilelor nu este zero este o linie dreaptă.]

7. Cum se numește rezolvarea unui sistem de ecuații cu două variabile?

[O soluție la un sistem de ecuații cu două variabile este o pereche de valori de variabile care transformă fiecare ecuație a sistemului într-o egalitate adevărată]

8. Ce înseamnă a rezolva un sistem de ecuații?

[A rezolva un sistem de ecuații înseamnă a-i găsi toate soluțiile sau a demonstra că nu există soluții.]

9. Aflați dacă un astfel de sistem are întotdeauna soluții și, dacă da, câte (grafic).

10. Câte soluții poate avea un sistem de două ecuații liniare cu două variabile?

[Singura soluție este dacă liniile se intersectează; nu are soluții dacă dreptele sunt paralele; infinit de multe dacă liniile coincid]

11. Ce ecuație definește de obicei o linie dreaptă?

12. Stabiliți o legătură între coeficienții unghiulari și termenii liberi:

Opțiunea I: y=-x+2 y= -x-3, k 1 = k 2, b 1 b 2, fără soluții;

Opțiunea II: y=-x+8 y=2x-1, k 1 k 2 , o soluţie;

Opțiunea III: y=-x-1 y=-x-1, k 1 = k 2, b 1 = b 2, multe soluții.

Concluzie:

1. Dacă coeficienții unghiulari ai dreptelor care sunt grafice ale acestor funcții sunt diferiți, atunci aceste drepte se intersectează și sistemul are o soluție unică.
2. Dacă coeficienții unghiulari ai dreptelor sunt aceiași, iar punctele de intersecție cu axa y sunt diferite, atunci liniile sunt paralele, iar sistemul nu are soluții.
3. Dacă coeficienții unghiulari și punctele de intersecție cu axa y sunt aceleași, atunci liniile coincid și sistemul are infinite de soluții.

Pe tablă există un tabel pe care profesorul și elevii îl completează treptat.

III. Explicarea unui subiect nou.

Definiție: sistem de vizualizare

• A1 x+B1 y=C
• A2x+B2y=C2

unde A 1, A 2, B 1, B 2, C 1 C 2 sunt expresii în funcție de parametri, iar x și y sunt necunoscute, se numește un sistem de două ecuații algebrice liniare cu două necunoscute în parametri.

Sunt posibile următoarele cazuri:

1) Dacă , atunci sistemul are o soluție unică

2) Dacă , atunci sistemul nu are soluții

3) Dacă , atunci sistemul are infinite de soluții.

IV. Consolidare

Exemplul 1.

La ce valori ale parametrului a are sistemul

• 2x - 3y = 7
• ah - 6y = 14

a) are un număr infinit de soluții;

b) are o soluție unică

Răspuns:

a) dacă a=4, atunci sistemul are un număr infinit de soluții;

b) dacă a4, atunci există o singură soluție.

Exemplul 2.

Rezolvați sistemul de ecuații

• x+(m+1)y=1
• x+2y=n

Rezolvare: a), i.e. pentru m1 sistemul are o soluție unică.

b), adică pentru m=1 (2=m+1) și n1 sistemul original nu are soluții

c) , pentru m=1 și n=1 sistemul are infinite soluții.

Răspuns: a) dacă m=1 și n1, atunci nu există soluții

b) m=1 și n=1, atunci soluția este o mulțime infinită

• y - oricare
• x=n-2y

c) dacă m1 și n sunt oricare, atunci

Exemplul 3.

• akh-3ау=2а+3
• x+ay=1

Rezolvare: Din ecuația II găsim x = 1-ay și înlocuim ecuația I în ecuație

а(1-ау)-3ау=2а+3

a-a 2 y-3ау=2а+3

A 2 y-3ау=а+3

A(a+3)y=a+3

Cazuri posibile:

1) a=0. Atunci ecuația arată ca 0*y=3 [y]

Prin urmare, pentru a=0 sistemul nu are soluții

2) a=-3. Atunci 0*y=0.

Prin urmare, y. În acest caz x=1-ау=1+3у

3) a0 și a-3. Atunci y=-, x=1-a(-=1+1=2

Răspuns:

1) dacă a=0, atunci (x; y)

2) dacă a=-3, atunci x=1+3y, y

3) dacă a0 și a?-3, apoi x=2, y=-

Să luăm în considerare a doua metodă de rezolvare a sistemului (1).

Să rezolvăm sistemul (1) folosind metoda adunării algebrice: în primul rând, înmulțim prima ecuație a sistemului cu B 2, a doua cu B 1 și adunăm aceste ecuații termen cu termen, eliminând astfel variabila y:

Deoarece A 1 B 2 -A 2 B 1 0, atunci x =

Acum să eliminăm variabila x. Pentru a face acest lucru, înmulțiți prima ecuație a sistemului (1) cu A 2 și a doua cu A 1 și adăugați ambele ecuații termen cu termen:

• A 1 A 2 x +A 2 B 1 y=A 2 C 1
• -A 1 A 2 x-A 1 B 2 y=-A 1 C 2
• y(A 2 B 1 -A 1 B 2) = A 2 C 1 -A 1 C 2

deoarece A 2 B 1 -A 1 B 2 0 y =

Pentru comoditatea rezolvării sistemului (1), introducem următoarea notație:

- determinant principal

Acum soluția sistemului (1) poate fi scrisă folosind determinanți:

Formulele date se numesc formule lui Cramer.

Dacă , atunci sistemul (1) are o soluție unică: x=; y=

Dacă , sau , atunci sistemul (1) nu are soluții

Dacă , , , , atunci sistemul (1) are un număr infinit de soluții.

În acest caz, sistemul trebuie investigat în continuare. În acest caz, de regulă, se reduce la o ecuație liniară. În acest caz, este adesea convenabil să studiem sistemul în felul următor: prin rezolvarea ecuației, găsim valori specifice ale parametrilor sau exprimăm unul dintre parametri în termenii celorlalți și înlocuim aceste valori ale parametrilor în sistemul. Apoi obținem un sistem cu coeficienți numerici specifici sau cu un număr mai mic de parametri, care trebuie studiat.

Dacă coeficienții A 1 , A 2 , B 1 , B 2 ai sistemului depind de mai mulți parametri, atunci este convenabil să se studieze sistemul folosind determinanți ai sistemului.

Exemplul 4.

Pentru toate valorile parametrului a, rezolvați sistemul de ecuații

• (a+5)x+(2a+3)y=3a+2
• (3a+10)x+(5a+6)y=2a+4

Soluție: Să găsim determinantul sistemului:

= (a+5)(5a+6) – (3a+10) (2a+3)= 5a 2 +31a+30-6a 2 -29a-30=-a 2 +2a=a(2-a)

= (3a+2) (5a+6) –(2a+4)(2a+3)=15a 2 +28a+12-4a 2 -14a-12=11a 2 +14a=a(11a+14)

=(a+5) (2a+4)-(3a+10)(3a+2)=2a 2 +14a+20-9a 2 -36a-20=-7a 2 -22a=-a(7a+22)

LA sarcini cu parametru Aceasta poate include, de exemplu, căutarea soluțiilor la ecuații liniare și pătratice în formă generală, studiul ecuației pentru numărul de rădăcini disponibile în funcție de valoarea parametrului.

Fără a oferi definiții detaliate, luați în considerare următoarele ecuații ca exemple:

y = kx, unde x, y sunt variabile, k este un parametru;

y = kx + b, unde x, y sunt variabile, k și b sunt parametri;

ax 2 + bx + c = 0, unde x sunt variabile, a, b și c sunt un parametru.

Rezolvarea unei ecuații (inegalitate, sistem) cu un parametru înseamnă, de regulă, rezolvarea unui set infinit de ecuații (inegalități, sisteme).

Sarcinile cu un parametru pot fi împărțite în două tipuri:

A) condiția spune: rezolvați ecuația (inegalitatea, sistemul) - aceasta înseamnă, pentru toate valorile parametrului, găsiți toate soluțiile. Dacă cel puțin un caz rămâne neinvestigat, o astfel de soluție nu poate fi considerată satisfăcătoare.

b) este necesar să se indice posibilele valori ale parametrului la care ecuația (inegalitatea, sistemul) are anumite proprietăți. De exemplu, are o soluție, nu are soluții, are soluții aparținând intervalului etc. În astfel de sarcini, este necesar să se indice clar la ce valoare a parametrului este îndeplinită condiția necesară.

Parametrul, fiind un număr fix necunoscut, are un fel de dualitate aparte. În primul rând, este necesar să se țină cont de faptul că faima presupusă indică faptul că parametrul trebuie perceput ca un număr. În al doilea rând, libertatea de a manipula parametrul este limitată de obscuritatea acestuia. De exemplu, operațiunile de împărțire la o expresie care conține un parametru sau de extragere a rădăcinii unui grad par dintr-o astfel de expresie necesită cercetări preliminare. Prin urmare, este necesară atenție la manipularea parametrului.

De exemplu, pentru a compara două numere -6a și 3a, trebuie să luați în considerare trei cazuri:

1) -6a va fi mai mare decât 3a dacă a este un număr negativ;

2) -6a = 3a în cazul în care a = 0;

3) -6a va fi mai mic decât 3a dacă a este un număr pozitiv 0.

Soluția va fi răspunsul.

Să fie dată ecuația kx = b. Această ecuație este o formă scurtă pentru un număr infinit de ecuații cu o variabilă.

La rezolvarea unor astfel de ecuații pot exista cazuri:

1. Fie k orice număr real care nu este egal cu zero și b orice număr din R, atunci x = b/k.

2. Fie k = 0 și b ≠ 0, ecuația inițială va lua forma 0 x = b. Evident, o astfel de ecuație nu are soluții.

3. Fie k și b numere egale cu zero, atunci avem egalitatea 0 x = 0. Soluția sa este orice număr real.

Algoritm pentru rezolvarea acestui tip de ecuație:

1. Determinați valorile de „control” ale parametrului.

2. Rezolvați ecuația inițială pentru x pentru valorile parametrilor care au fost determinate în primul paragraf.

3. Rezolvați ecuația inițială pentru x pentru valorile parametrilor diferite de cele alese în primul paragraf.

4. Puteți scrie răspunsul în următoarea formă:

1) pentru ... (valorile parametrilor), ecuația are rădăcini ...;

2) pentru ... (valorile parametrilor), nu există rădăcini în ecuație.

Exemplul 1.

Rezolvați ecuația cu parametrul |6 – x| = a.

Soluţie.

Este ușor de observat că aici a ≥ 0.

Conform regulii modulului 6 – x = ±a, exprimăm x:

Răspuns: x = 6 ± a, unde a ≥ 0.

Exemplul 2.

Rezolvați ecuația a(x – 1) + 2(x – 1) = 0 în raport cu variabila x.

Soluţie.

Să deschidem parantezele: aх – а + 2х – 2 = 0

Să scriem ecuația în formă standard: x(a + 2) = a + 2.

Dacă expresia a + 2 nu este zero, adică dacă a ≠ -2, avem soluția x = (a + 2) / (a ​​+ 2), adică. x = 1.

Dacă a + 2 este egal cu zero, i.e. a = -2, atunci avem egalitatea corectă 0 x = 0, deci x este orice număr real.

Răspuns: x = 1 pentru a ≠ -2 și x € R pentru a = -2.

Exemplul 3.

Rezolvați ecuația x/a + 1 = a + x în raport cu variabila x.

Soluţie.

Dacă a = 0, atunci transformăm ecuația în forma a + x = a 2 + ax sau (a – 1)x = -a(a – 1). Ultima ecuație pentru a = 1 are forma 0 x = 0, prin urmare x este orice număr.

Dacă a ≠ 1, atunci ultima ecuație va lua forma x = -a.

Această soluție poate fi ilustrată pe linia de coordonate (Fig. 1)

Răspuns: nu există soluții pentru a = 0; x – orice număr cu a = 1; x = -a pentru a ≠ 0 și a ≠ 1.

Metoda grafica

Să luăm în considerare o altă modalitate de a rezolva ecuațiile cu un parametru - grafic. Această metodă este folosită destul de des.

Exemplul 4.

În funcție de parametrul a, câte rădăcini are ecuația ||x| – 2| = a?

Soluţie.

Pentru a rezolva folosind metoda grafică, construim grafice ale funcțiilor y = ||x| – 2| și y = a (Fig. 2).

Desenul arată în mod clar cazurile posibile de locație a dreptei y = a și numărul de rădăcini din fiecare dintre ele.

Răspuns: ecuația nu va avea rădăcini dacă a< 0; два корня будет в случае, если a >2 și a = 0; ecuația va avea trei rădăcini în cazul a = 2; patru rădăcini - la 0< a < 2.

Exemplul 5.

La ce este ecuația 2|x| + |x – 1| = a are o singură rădăcină?

Soluţie.

Să descriem graficele funcțiilor y = 2|x| + |x – 1| și y = a. Pentru y = 2|x| + |x – 1|, extinzând modulele folosind metoda intervalului, obținem:

(-3x + 1, la x< 0,

y = (x + 1, pentru 0 ≤ x ≤ 1,

(3x – 1, pentru x > 1.

Pe Figura 3 Se vede clar că ecuația va avea o singură rădăcină numai atunci când a = 1.

Răspuns: a = 1.

Exemplul 6.

Determinați numărul de soluții ale ecuației |x + 1| + |x + 2| = a în funcție de parametrul a?

Soluţie.

Graficul funcției y = |x + 1| + |x + 2| va fi o linie întreruptă. Vârfurile sale vor fi situate în punctele (-2; 1) și (-1; 1) (Figura 4).

Răspuns: dacă parametrul a este mai mic de unu, atunci ecuația nu va avea rădăcini; dacă a = 1, atunci soluția ecuației este o mulțime infinită de numere din segmentul [-2; -1]; dacă valorile parametrului a sunt mai mari decât unu, atunci ecuația va avea două rădăcini.

Mai ai întrebări? Nu știi cum să rezolvi ecuații cu un parametru?
Pentru a primi ajutor de la un tutor -.
Prima lecție este gratuită!

blog.site, atunci când copiați materialul integral sau parțial, este necesar un link către sursa originală.

Utilizarea ecuațiilor este larg răspândită în viața noastră. Ele sunt folosite în multe calcule, construcție de structuri și chiar sport. Omul a folosit ecuații în antichitate, iar de atunci utilizarea lor a crescut. În matematică, există probleme în care este necesar să se caute soluții la ecuații liniare și pătratice în formă generală sau să se caute numărul de rădăcini pe care le are o ecuație în funcție de valoarea unui parametru. Toate aceste sarcini au parametri.

Luați în considerare următoarele ecuații ca exemplu ilustrativ:

\[y = kx,\] unde \ sunt variabile, \ este un parametru;

\[y = kx + b,\] unde \ sunt variabile, \ este un parametru;

\[аx^2 + bх + с = 0,\] unde \ este o variabilă, \[а, b, с\] este un parametru.

Rezolvarea unei ecuații cu un parametru înseamnă, de regulă, rezolvarea unui set infinit de ecuații.

Cu toate acestea, urmând un anumit algoritm, puteți rezolva cu ușurință următoarele ecuații:

1. Determinați valorile de „control” ale parametrului.

2. Rezolvați ecuația inițială pentru [\x\] cu valorile parametrilor definite în primul paragraf.

3. Rezolvați ecuația inițială pentru [\x\] pentru valorile parametrilor diferite de cele alese în primul paragraf.

Să presupunem că ni se dă următoarea ecuație:

\[\mid 6 - x \mid = a.\]

După ce am analizat datele inițiale, este clar că un \[\ge 0.\]

Conform regulii modulului \ exprimăm \

Răspuns: \unde\

Unde pot rezolva o ecuație cu un parametru online?

Puteți rezolva ecuația pe site-ul nostru https://site. Rezolvatorul online gratuit vă va permite să rezolvați ecuații online de orice complexitate în câteva secunde. Tot ce trebuie să faceți este să introduceți pur și simplu datele dvs. în soluție. De asemenea, puteți viziona instrucțiuni video și puteți afla cum să rezolvați ecuația pe site-ul nostru. Și dacă mai aveți întrebări, le puteți adresa în grupul nostru VKontakte http://vk.com/pocketteacher. Alătură-te grupului nostru, suntem mereu bucuroși să te ajutăm.

Notă. În exemplul dat, calculul tuturor determinanților s-a încheiat cu o reprezentare sub forma unui produs de factori, dintre care unul (13) a fost redus în timpul împărțirii. Această situație este foarte comună. Prin urmare, nu este nevoie să vă grăbiți să înmulțiți factorii, deși cel mai adesea aceștia nu se anulează.

Problema 4.4. Rezolvați sisteme de ecuații folosind regula lui Cramer:

	1 + 4x 2 + x 3 = 21			1 + x 2 − x 3 = 2	2x 1 + x 2 + x 3 = 7
				3x 2 − 3x3 = 1
1) 4x1 + 2x2 + x3 = 27					3) x1 + 4x2 − 5x3
	3x2 + 2x3 = 19			− 2x2 + 3x3 = 7
					4x1 + 10x2 − x3

Rezolvarea problemelor de mai sus arată că formulele lui Cramer reprezintă o metodă unificată și convenabilă pentru găsirea soluțiilor sistemelor de ecuații liniare.

Notă. Utilizarea formulelor lui Cramer este mult simplificată dacă trebuie să găsiți doar una dintre necunoscute: în acest caz, trebuie să numărați doar doi determinanți.

2.4.4. Sisteme de ecuații cu parametri

Mai sus, au fost luate în considerare sistemele de ecuații algebrice liniare cu coeficienți fix pentru necunoscute și părțile din dreapta ale ecuațiilor. În problemele practice, de foarte multe ori acești coeficienți și valorile părților din dreapta nu sunt cunoscute cu exactitate. Prin urmare, este necesar să se analizeze influența unor astfel de parametri asupra soluției sistemelor.

Exemplul 4.5. Investigați dependența soluției de un sistem de ecuații

3 x + 8 y = a5 x + 9 y = b

din parametrii a și b.

Aici, numai părțile din dreapta ale ecuațiilor depind de parametri. Deoarece

							27 − 40 = − 13 ≠ 0

Pentru a găsi o soluție, puteți folosi formulele lui Cramer. Avem:

∆1				9a − 8b,∆ 2				3b−5a

x = x

= ∆ 1

9a−8b

8b−9a

Y=x

∆ 2 =

5a−3b

− 13

Prin înlocuire ne asigurăm că soluția rezultată este corectă:

8b−9a

5a−3b

a(− 27 + 40)

B(24 − 24)

8b−9a

5a−3b

a(− 45 + 45)

− 27)

În special, dacă a = 11, b = 14 obținem: x =

8×14 − 9×11

1 și y = 1.

y(a, b)

x(a, b)

Astfel, fiecare pereche de parametri a și b corespunde unei perechi unice de numere x și y care satisface sistemul dat de ecuații. Aceasta înseamnă că soluția sistemului de ecuații este o pereche ordonată și două funcții a două variabile (parametrii a și b). Ambele funcții sunt definite pentru orice valoare a acestor parametri și depind liniar de variabilele independente a și b. În plus, x crește monoton

funcția de topire b și funcția de descreștere monotonică a,					- viceversa,
o funcție crescătoare a și o funcție monoton descrescătoare b.
Problema 4.5. Găsiți soluții la sistemele de ecuații
8 x + 5 y = 2 a + 1	4 x + 9 y = a + b	9x + 4 y
3 x + 2 y = a	3 x + 8 y = 3 a − b	8 x + 3 y

și explorați dependența soluției lor de parametrii a și b. Recomandare. Trasează grafice ale soluțiilor rezultate x (a, b) și y (a, b)

ca funcţii ale parametrilor variabili a şi b. Explicați de ce în toate problemele soluțiile depind liniar de parametrii a și b.

Exemplul 4.6. Investigați dependența soluției de un sistem de ecuații

			(a + 3) x + 2 ay = 5
din parametrii a și b.					x + 5 y = b
În acest exemplu, coeficienții pentru necunoscute depind de parametru
a , iar laturile drepte sunt din parametrul b .
Să găsim determinantul matricei coeficienților pentru necunoscute:
		a + 3 2			5(a + 3) − 2a = 3(a + 5)

Acest determinant nu este egal cu zero numai atunci când a ≠ − 5. Prin urmare, formulele lui Cramer pot fi utilizate numai când a ≠ − 5. În acest caz:

∆1 =					25 − 2ab , ∆ 2 =		a+3			Ab + 3b − 5

x = x		25 − 2ab	y = x			3 b − 5 + ab
		3(a+5)				3(a+5)

Să considerăm separat cazul a = − 5. Atunci sistemul original este:

− 2 x −10 y = 5 x +5 y = b

− 5 − c x = c , y = 2

Desigur, există arbitrar în alegerea valorii oricăreia dintre necunoscute, iar soluția poate fi scrisă și sub forma:

x = − 5 2 − 5 c , y = c

Astfel, dependența de parametrul coeficienților pentru necunoscutele sistemului original poate da naștere la absența unei soluții sau la prezența unui număr infinit de soluții. Faptul descoperit este o generalizare a ceea ce era cunoscut anterior pentru o ecuație ax = b și pentru sisteme de două ecuații liniare cu două necunoscute.

Observația 1. Introducerea constantei c în soluția unui sistem de ecuații seamănă cu arbitrarul în alegerea constantei de integrare.

Nota 2. Exemplul luat în considerare arată că, ca și pentru o ecuație, pentru sistemele algebrice liniare cu un număr mare de ecuații și necunoscute, sunt posibile doar trei cazuri diferite: o singură soluție, nicio soluție sau infinit de soluții.

Problema 4.6. Explorați soluțiile sistemului de ecuații:

4 x + 5 ay = 2 a		4 x + 5 ay = 2 a			4 x + 5 ay = 2 a
8 x + 10 y		8 x + 10 y			8 x + 10 y = b

Problema 4.7. Vino cu propriul tău sistem de două ecuații algebrice cu două necunoscute și doi parametri și studiază-l în funcție de valorile parametrilor.

Întrebări pentru autocontrol

1) Care este minorul unui element determinant?

2) Care este diferența dintre complementul algebric și elementul minor al unui determinant?

3) Ce este o matrice adjunctă?

4) Cum să găsiți matricea adjunctă pentru o matrice dată?

5) Care este ordinea matricei adiacente?

6) În ce caz nu există matricea inversă?

7) Care matrice se numește nesingular?

8) În ce condiții pot fi utilizate formulele lui Cramer?

9) Care este soluția unui sistem de ecuații algebrice liniare?

10) Ce determinanți sunt incluși în formulele lui Cramer?

11) Când depind determinanții de parametri?

12) Produsul matricei adiacente și matricea originală poate fi o matrice scalară?

13) Cum afectează rearanjarea factorilor rezultatul la înmulțirea matricei adiacente și a matricei originale?

14) Care sunt formulele lui Cramer?

15) În ce condiții poate fi găsită o soluție a unui sistem de ecuații algebrice liniare folosind regula lui Cramer (formule)?