Cum ?
Exemple de soluții

Dacă ceva lipsește undeva, înseamnă că este ceva undeva

Continuăm să studiem secțiunea „Funcții și grafice”, iar următoarea stație din călătoria noastră este. O discuție activă a acestui concept a început în articolul despre seturi și a continuat în prima lecție despre grafice de funcții, unde am analizat funcțiile elementare și, în special, domeniile lor de definiție. Prin urmare, recomand ca manechinele să înceapă cu elementele de bază ale subiectului, deoarece nu mă voi opri din nou asupra unor puncte de bază.

Se presupune că cititorul cunoaște domeniul de definire al următoarelor funcții: funcții liniare, pătratice, cubice, polinoame, exponențiale, sinus, cosinus. Ele sunt definite pe (mulțimea tuturor numerelor reale). Pentru tangente, arcsinus, așa să fie, vă iert =) - graficele mai rare nu sunt amintite imediat.

Sfera de aplicare pare a fi un lucru simplu și apare o întrebare logică: despre ce va fi articolul? În această lecție mă voi uita la problemele comune de găsire a domeniului unei funcții. Mai mult, vom repeta inegalități cu o variabilă, ale căror abilități de rezolvare vor fi cerute și în alte probleme de matematică superioară. Materialul, apropo, este tot material școlar, așa că va fi util nu numai elevilor, ci și elevilor. Informațiile, desigur, nu pretind a fi enciclopedice, dar aici nu sunt exemple exagerate de „moarte”, ci castane prăjite, care sunt preluate din adevărate lucrări practice.

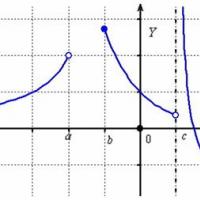
Să începem cu o scufundare rapidă în subiect. Pe scurt despre principalul lucru: vorbim despre o funcție a unei variabile. Domeniul său de definire este multe sensuri ale lui "x", pentru care exista sensuri ale „jucătorilor”. Să ne uităm la un exemplu ipotetic:

Domeniul de definire al acestei funcții este o uniune de intervale:
(pentru cei care au uitat: - pictograma unirii). Cu alte cuvinte, dacă luați orice valoare a lui „x” din intervalul , sau din , sau din , atunci pentru fiecare astfel de „x” va exista o valoare „y”.

În linii mari, acolo unde este domeniul definiției, există un grafic al funcției. Dar semi-intervalul și punctul „tse” nu sunt incluse în zona de definiție și nu există nici un grafic acolo.

Cum se găsește domeniul unei funcții? Mulți oameni își amintesc rima pentru copii: „piatră, hârtie, foarfece”, iar în acest caz poate fi parafrazată în siguranță: „rădăcină, fracție și logaritm”. Astfel, dacă întâlnești o fracțiune, rădăcină sau logaritm pe calea vieții tale, ar trebui să fii imediat foarte, foarte precaut! Tangenta, cotangente, arcsinus, arccosinus sunt mult mai puțin frecvente și vom vorbi și despre ele. Dar mai întâi, schițe din viața furnicilor:

Domeniul unei funcții care conține o fracție

Să presupunem că ni se dă o funcție care conține o fracție. După cum știți, nu puteți împărți la zero: , deci acelea Valorile „X” care transformă numitorul la zero nu sunt incluse în domeniul de aplicare al acestei funcții.

Nu mă voi opri asupra celor mai simple funcții precum etc., deoarece toată lumea vede perfect punctele care nu sunt incluse în domeniul său de definire. Să ne uităm la fracții mai semnificative:

Exemplul 1

Găsiți domeniul unei funcții

Soluţie: Nu există nimic special în numărător, dar numitorul trebuie să fie diferit de zero. Să-l setăm egal cu zero și să încercăm să găsim punctele „rele”:

Ecuația rezultată are două rădăcini: . Valorile datelor nu fac parte din domeniul de aplicare al funcției. Într-adevăr, înlocuiți sau în funcție și veți vedea că numitorul ajunge la zero.

Răspuns: domeniul de aplicare al definiției:

Intrarea sună astfel: „domeniul de definiție este toate numerele reale, cu excepția mulțimii constând din valori " Permiteți-mi să vă reamintesc că simbolul barei oblice inverse în matematică denotă scăderea logică, iar parantezele denotă set. Răspunsul poate fi scris în mod echivalent ca o uniune a trei intervale:

Cui îi place.

La puncte funcția tolerează pauze nesfârșite, și dreptele date de ecuații sunt asimptote verticale pentru graficul acestei funcţii. Cu toate acestea, acesta este un subiect ușor diferit și nu mă voi concentra mai departe asupra acestui subiect.

Exemplul 2

Găsiți domeniul unei funcții

Sarcina este în esență orală și mulți dintre voi veți găsi aproape imediat zona de definiție. Răspunsul este la sfârșitul lecției.

Va fi întotdeauna o fracțiune „rea”? Nu. De exemplu, o funcție este definită pe întreaga linie numerică. Indiferent de valoarea lui „x” luăm, numitorul nu va merge la zero, în plus, va fi întotdeauna pozitiv: . Astfel, sfera acestei funcții este: .

Toate funcțiile ca definite şi continuu pe .

Situația este puțin mai complicată când numitorul este ocupat de un trinom pătratic:

Exemplul 3

Găsiți domeniul unei funcții

Soluţie: Să încercăm să găsim punctele în care numitorul ajunge la zero. Pentru asta vom decide ecuație pătratică:

Discriminantul s-a dovedit a fi negativ, ceea ce înseamnă că nu există rădăcini reale, iar funcția noastră este definită pe întreaga axă a numerelor.

Răspuns: domeniul de aplicare al definiției:

Exemplul 4

Găsiți domeniul unei funcții

Acesta este un exemplu de rezolvat singur. Soluția și răspunsul sunt la sfârșitul lecției. Vă sfătuiesc să nu fi leneș cu probleme simple, deoarece neînțelegerile se vor acumula cu alte exemple.

Domeniul unei funcții cu rădăcină

Funcția rădăcină pătrată este definită numai pentru acele valori ale lui „x” când expresia radicală este nenegativă: . Dacă rădăcina este situată în numitor , atunci condiția este în mod evident strânsă: . Calcule similare sunt valabile pentru orice rădăcină de grad par pozitiv: , totuși, rădăcina este deja de gradul 4 în studii functionale Nu-mi amintesc.

Exemplul 5

Găsiți domeniul unei funcții

Soluţie: expresia radicală trebuie să fie nenegativă:

Înainte de a continua cu soluția, permiteți-mi să vă reamintesc regulile de bază pentru lucrul cu inegalitățile, cunoscute de la școală.

Acord o atenție deosebită! Acum luăm în considerare inegalitățile cu o variabilă- adică doar pentru noi există o dimensiune de-a lungul axei. Vă rugăm să nu confundați cu inegalitățile a două variabile, unde întregul plan de coordonate este implicat geometric. Totuși, există și coincidențe plăcute! Deci, pentru inegalitate, următoarele transformări sunt echivalente:

1) Condițiile pot fi transferate dintr-o parte în parte prin modificarea lor (termenii) semne.

2) Ambele părți ale inegalității pot fi înmulțite cu un număr pozitiv.

3) Dacă ambele părți ale inegalității sunt înmulțite cu negativ numărul, atunci trebuie să îl schimbați semn al inegalității în sine. De exemplu, dacă a existat „mai mult”, atunci va deveni „mai puțin”; dacă a fost „mai mic decât sau egal”, atunci va deveni „mai mare decât sau egal”.

În inegalitate, mutam „trei” în partea dreaptă cu o schimbare de semn (regula nr. 1):

Să înmulțim ambele părți ale inegalității cu –1 (regula nr. 3):

Să înmulțim ambele părți ale inegalității cu (regula nr. 2):

Răspuns: domeniul de aplicare al definiției:

Răspunsul poate fi scris și într-o frază echivalentă: „funcția este definită la ”.
Geometric, zona de definire este reprezentată prin umbrirea intervalelor corespunzătoare pe axa absciselor. În acest caz:

Încă o dată vă reamintesc de semnificația geometrică a domeniului de definiție - graficul funcției există doar în zona umbrită și lipsește la .

În cele mai multe cazuri, o determinare pur analitică a domeniului de definiție este potrivită, dar atunci când funcția este foarte complicată, ar trebui să desenați o axă și să faceți note.

Exemplul 6

Găsiți domeniul unei funcții

Acesta este un exemplu de rezolvat singur.

Când există un binom pătrat sau un trinom sub rădăcina pătrată, situația devine puțin mai complicată, iar acum vom analiza în detaliu tehnica soluției:

Exemplul 7

Găsiți domeniul unei funcții

Soluţie: expresia radicală trebuie să fie strict pozitivă, adică trebuie să rezolvăm inegalitatea. La primul pas, încercăm să factorăm trinomul pătratic:

Discriminantul este pozitiv, căutăm rădăcini:

Deci parabola intersectează axa absciselor în două puncte, ceea ce înseamnă că o parte a parabolei este situată sub axă (inegalitatea), iar o parte a parabolei este situată deasupra axei (inegalitatea de care avem nevoie).

Deoarece coeficientul este , ramurile parabolei sunt îndreptate în sus. Din cele de mai sus rezultă că inegalitatea este satisfăcută pe intervale (ramurile parabolei merg în sus la infinit), iar vârful parabolei este situat pe intervalul de sub axa x, care corespunde inegalității:

! Nota: Dacă nu înțelegeți pe deplin explicațiile, vă rugăm să desenați a doua axă și întreaga parabola! Este recomandabil să reveniți la articol și manual Formule fierbinți pentru cursul școlar de matematică.

Vă rugăm să rețineți că punctele în sine sunt eliminate (nu sunt incluse în soluție), deoarece inegalitatea noastră este strictă.

Răspuns: domeniul de aplicare al definiției:

În general, multe inegalități (inclusiv cea considerată) sunt rezolvate de universal metoda intervalului, cunoscut din nou din programa școlară. Dar în cazul binoamelor pătrate și trinoamelor, după părerea mea, este mult mai convenabil și mai rapid să analizăm locația parabolei în raport cu axa. Și vom analiza metoda principală - metoda intervalului - în detaliu în articol. Zerourile funcției. Intervale de constanță.

Exemplul 8

Găsiți domeniul unei funcții

Acesta este un exemplu de rezolvat singur. Eșantionul comentează în detaliu logica raționamentului + a doua metodă de rezolvare și o altă transformare importantă a inegalității, fără cunoștință de care elevul va șchiopăta pe un picior..., ...hmm... poate m-am entuziasmat despre picior, mai probabil pe un deget. Degetul mare.

Poate fi definită o funcție rădăcină pătrată pe întreaga linie numerică? Cu siguranţă. Toate fețele cunoscute: . Sau o sumă similară cu un exponent: . Într-adevăr, pentru orice valoare a lui „x” și „ka”: , prin urmare și .

Iată un exemplu mai puțin evident: . Aici discriminantul este negativ (parabola nu intersectează axa x), în timp ce ramurile parabolei sunt îndreptate în sus, de unde și domeniul de definiție: .

Întrebarea opusă: poate fi domeniul de definire al unei funcții gol? Da, și un exemplu primitiv se sugerează imediat , unde expresia radicală este negativă pentru orice valoare a lui „x”, iar domeniul de definiție: (pictogramă set gol). O astfel de funcție nu este deloc definită (desigur, graficul este și iluzoriu).

Cu rădăcini ciudate etc. totul este mult mai bine - aici expresia radicală poate fi negativă. De exemplu, o funcție este definită pe întreaga linie numerică. Cu toate acestea, funcția are un singur punct care încă nu este inclus în domeniul definiției, deoarece numitorul este setat la zero. Din același motiv pentru funcție punctele sunt excluse.

Domeniul unei funcții cu un logaritm

A treia funcție comună este logaritmul. Ca exemplu, voi desena logaritmul natural, care apare în aproximativ 99 de exemple din 100. Dacă o anumită funcție conține un logaritm, atunci domeniul său de definiție ar trebui să includă doar acele valori ale lui „x” care satisfac inegalitatea. Dacă logaritmul este la numitor: , atunci în plus se impune o condiție (din moment ce ).

Exemplul 9

Găsiți domeniul unei funcții

Soluţie: în conformitate cu cele de mai sus, vom compune și rezolva sistemul:

Soluție grafică pentru manechine:

Răspuns: domeniul de aplicare al definiției:

Mă voi opri asupra unui alt punct tehnic - nu am scara indicată și diviziunile de-a lungul axei nu sunt marcate. Se pune întrebarea: cum să faci astfel de desene într-un caiet pe hârtie în carouri? Distanța dintre puncte ar trebui măsurată de celule strict în funcție de scară? Este mai canonic și mai strict, desigur, la scară, dar un desen schematic care reflectă în mod fundamental situația este, de asemenea, destul de acceptabil.

Exemplul 10

Găsiți domeniul unei funcții

Pentru a rezolva problema, puteți utiliza metoda din paragraful anterior - analizați modul în care parabola este situată în raport cu axa x. Răspunsul este la sfârșitul lecției.

După cum puteți vedea, în domeniul logaritmilor totul este foarte asemănător cu situația cu rădăcini pătrate: funcția (trinomul pătrat din Exemplul nr. 7) este definit pe intervale, iar funcția (binomul pătrat din Exemplul nr. 6) pe intervalul . Este incomod chiar să spunem că funcțiile de tip sunt definite pe întreaga linie numerică.

Informații utile : funcția tipică este interesantă, este definită pe întreaga linie numerică cu excepția punctului. Conform proprietății logaritmului, „doi” pot fi înmulțiți în afara logaritmului, dar pentru ca funcția să nu se schimbe, „x” trebuie să fie inclus sub semnul modulului: . Iată o altă „aplicație practică” a modulului =). Aceasta este ceea ce trebuie să faceți în majoritatea cazurilor când demolați chiar grad, de exemplu: . Dacă baza gradului este evident pozitivă, de exemplu, atunci nu este nevoie de semnul modulului și este suficient să folosiți paranteze: .

Pentru a evita repetarea, să complicăm sarcina:

Exemplul 11

Găsiți domeniul unei funcții

Soluţie: în această funcție avem atât rădăcina cât și logaritmul.

Expresia radicală trebuie să fie nenegativă: , iar expresia sub semnul logaritmului trebuie să fie strict pozitivă: . Astfel, este necesar să se rezolve sistemul:

Mulți dintre voi știu foarte bine sau ghiciți intuitiv că soluția de sistem trebuie să satisfacă tuturor stare.

Examinând locația parabolei față de axă, ajungem la concluzia că inegalitatea este satisfăcută de intervalul (umbrire albastră):

Inegalitatea corespunde în mod evident semiintervalului „roșu”.

Deoarece ambele condiții trebuie îndeplinite simultan, atunci soluția sistemului este intersecția acestor intervale. „Interesele comune” sunt îndeplinite la pauză.

Răspuns: domeniul de aplicare al definiției:

Inegalitatea tipică, așa cum este demonstrată în Exemplul nr. 8, nu este dificil de rezolvat analitic.

Domeniul găsit nu se va modifica pentru „funcții similare”, de ex. sau . De asemenea, puteți adăuga câteva funcții continue, de exemplu: , sau astfel: , sau chiar așa: . După cum se spune, rădăcina și logaritmul sunt lucruri încăpățânate. Singurul lucru este că, dacă una dintre funcții este „resetată” la numitor, atunci domeniul de definiție se va schimba (deși în cazul general acest lucru nu este întotdeauna adevărat). Ei bine, în teoria matan despre acest verbal... oh... există teoreme.

Exemplul 12

Găsiți domeniul unei funcții

Acesta este un exemplu de rezolvat singur. Utilizarea unui desen este destul de potrivită, deoarece funcția nu este cea mai simplă.

Încă câteva exemple pentru a consolida materialul:

Exemplul 13

Găsiți domeniul unei funcții

Soluţie: să compunem și să rezolvăm sistemul:

Toate acțiunile au fost deja discutate pe parcursul articolului. Să descriem intervalul corespunzător inegalității pe dreapta numerică și, conform celei de-a doua condiții, eliminăm două puncte:

Sensul s-a dovedit a fi complet irelevant.

Răspuns: domeniu de definire

Un mic joc de matematică pe o variație a celui de-al 13-lea exemplu:

Exemplul 14

Găsiți domeniul unei funcții

Acesta este un exemplu de rezolvat singur. Cei care au ratat-o ​​au ghinion ;-)

Secțiunea finală a lecției este dedicată funcțiilor mai rare, dar și „de lucru”:

Zone de definire a funcției
cu tangente, cotangente, arcsinus, arccosinus

Dacă o funcție include , atunci din domeniul său de definiție exclus puncte , Unde Z– un set de numere întregi. În special, așa cum se menționează în articol Grafice și proprietăți ale funcțiilor elementare, funcția are următoarele valori:

Adică domeniul de definire al tangentei: .

Să nu ucidem prea mult:

Exemplul 15

Găsiți domeniul unei funcții

Soluţie: în acest caz, următoarele puncte nu vor fi incluse în domeniul definiției:

Să aruncăm „doi” din partea stângă în numitorul din dreapta:

Ca urmare :

Răspuns: domeniul de aplicare al definiției: .

În principiu, răspunsul poate fi scris ca o unire a unui număr infinit de intervale, dar construcția va fi foarte greoaie:

Soluția analitică este complet în concordanță cu transformarea geometrică a graficului: dacă argumentul unei funcții este înmulțit cu 2, atunci graficul acesteia se va micșora la axă de două ori. Observați cum perioada funcției a fost redusă la jumătate și puncte de pauză dublat în frecvență. tahicardie.

O poveste similară cu cotangent. Dacă o funcție include , atunci punctele sunt excluse din domeniul său de definire. În special, pentru funcția de explozie automată filmăm următoarele valori:

Cu alte cuvinte:

Când rezolvăm diverse probleme, de foarte multe ori trebuie să efectuăm transformări identice ale expresiilor. Dar se întâmplă că un fel de transformare este acceptabil în unele cazuri, dar nu în altele. Asistență semnificativă în ceea ce privește monitorizarea admisibilității transformărilor în curs este oferită de ODZ. Să ne uităm la asta mai detaliat.

Esența abordării este următoarea: ODZ a variabilelor pentru expresia originală este comparată cu ODZ a variabilelor pentru expresia obținută ca urmare a transformărilor identice, iar pe baza rezultatelor comparației se trag concluzii adecvate.

În general, transformările identitare pot

• nu influențează DL;
• duce la extinderea ODZ;
• duce la o îngustare a ODZ.

Să ilustrăm fiecare caz cu un exemplu.

Luați în considerare expresia x 2 +x+3·x, ODZ a variabilei x pentru această expresie este mulțimea R. Acum să facem următoarea transformare identică cu această expresie - prezentăm termeni similari, ca rezultat va lua forma x 2 +4·x. Evident, variabila x a acestei expresii este și o mulțime R. Astfel, transformarea efectuată nu a schimbat DZ.

Să mergem mai departe. Să luăm expresia x+3/x−3/x. În acest caz, ODZ este determinată de condiția x≠0, care corespunde mulțimii (−∞, 0)∪(0, +∞) . Această expresie conține, de asemenea, termeni similari, după reducerea cărora ajungem la expresia x, pentru care ODZ este R. Ce vedem: ca urmare a transformării, ODZ a fost extins (numărul zero a fost adăugat la ODZ al variabilei x pentru expresia originală).

Rămâne de luat în considerare un exemplu de restrângere a intervalului de valori acceptabile după transformări. Să luăm expresia . ODZ a variabilei x este determinată de inegalitatea (x−1)·(x−3)≥0, pentru soluția sa este potrivită, de exemplu, ca rezultat avem (−∞, 1]∪∪; editat de S. A. Telyakovsky - 17- ed. - M.: Educaţie, 2008. - 240 p.: ISBN 978-5-09-019315-3.

Mordkovich A.G. Algebră. clasa a VII-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich. - Ed. a XVII-a, add. - M.: Mnemosyne, 2013. - 175 p.: ill. ISBN 978-5-346-02432-3.

Mordkovich A.G. Algebră. clasa a 8-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich. - Ed. a XI-a, șters. - M.: Mnemosyne, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.

Mordkovich A.G. Algebră. clasa a 9-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich, P. V. Semenov. - Ed. a XIII-a, șters. - M.: Mnemosyne, 2011. - 222 p.: ill. ISBN 978-5-346-01752-3.

Mordkovich A.G. Algebra și începuturile analizei matematice. clasa a XI-a. În 2 ore. Partea 1. Manual pentru studenții instituțiilor de învățământ general (nivel de profil) / A. G. Mordkovich, P. V. Semenov. - Ed. a II-a, șters. - M.: Mnemosyne, 2008. - 287 p.: ill. ISBN 978-5-346-01027-2.

Algebrăși începutul analizei matematice. Clasa a X-a: manual. pentru invatamantul general instituţii: de bază şi de profil. niveluri / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; editat de A. B. Jiţcenko. - Ed. a 3-a. - M.: Educație, 2010.- 368 p. : ill. - ISBN 978-5-09-022771-1.

Orice expresie cu o variabilă are propriul interval de valori valide, acolo unde există. ODZ trebuie întotdeauna luat în considerare la luarea deciziilor. Dacă este absent, este posibil să obțineți un rezultat incorect.

Acest articol va arăta cum să găsiți corect ODZ și să folosiți exemple. Se va discuta, de asemenea, importanța indicarii DZ la luarea unei decizii.

Valori variabile valide și nevalide

Această definiție este legată de valorile permise ale variabilei. Când introducem definiția, să vedem la ce rezultat va duce.

Începând din clasa a VII-a începem să lucrăm cu numere și expresii numerice. Definițiile inițiale cu variabile trec la sensul expresiilor cu variabilele selectate.

Când există expresii cu variabile selectate, este posibil ca unele dintre ele să nu fie satisfăcute. De exemplu, o expresie de forma 1: a, dacă a = 0, atunci nu are sens, deoarece este imposibil de împărțit la zero. Adică, expresia trebuie să aibă valori care să fie potrivite în orice caz și să dea un răspuns. Cu alte cuvinte, au sens cu variabilele existente.

Definiția 1

Dacă există o expresie cu variabile, atunci are sens numai dacă valoarea poate fi calculată prin înlocuirea lor.

Definiția 2

Dacă există o expresie cu variabile, atunci nu are sens când, la înlocuirea lor, valoarea nu poate fi calculată.

Adică, aceasta implică o definiție completă

Definiția 3

Variabilele admisibile existente sunt acele valori pentru care expresia are sens. Și dacă nu are sens, atunci sunt considerate inacceptabile.

Pentru a clarifica cele de mai sus: dacă există mai multe variabile, atunci poate exista o pereche de valori adecvate.

Exemplul 1

De exemplu, luați în considerare o expresie de forma 1 x - y + z, unde există trei variabile. În caz contrar, îl puteți scrie ca x = 0, y = 1, z = 2, în timp ce o altă intrare are forma (0, 1, 2). Aceste valori sunt numite valide, ceea ce înseamnă că valoarea expresiei poate fi găsită. Obținem că 1 0 - 1 + 2 = 1 1 = 1. Din aceasta vedem că (1, 1, 2) sunt inacceptabile. Înlocuirea are ca rezultat împărțirea la zero, adică 1 1 - 2 + 1 = 1 0.

Ce este ODZ?

Gama de valori acceptabile este un element important atunci când se evaluează expresii algebrice. Prin urmare, merită să acordați atenție acestui lucru atunci când faceți calcule.

Definiția 4

zona ODZ este setul de valori permise pentru o expresie dată.

Să ne uităm la un exemplu de expresie.

Exemplul 2

Dacă avem o expresie de forma 5 z - 3, atunci ODZ are forma (− ∞, 3) ∪ (3, + ∞) . Acesta este intervalul de valori valide care satisface variabila z pentru o anumită expresie.

Dacă există expresii de forma z x - y, atunci este clar că x ≠ y, z ia orice valoare. Aceasta se numește expresii ODZ. Trebuie luată în considerare pentru a nu obține împărțirea la zero la înlocuire.

Intervalul de valori admisibile și domeniul de definiție au același sens. Doar al doilea dintre ele este folosit pentru expresii, iar primul este folosit pentru ecuații sau inegalități. Cu ajutorul DL, expresia sau inegalitatea are sens. Domeniul de definire al funcției coincide cu intervalul de valori admisibile ale variabilei x pentru expresia f (x).

Cum să găsești ODZ? Exemple, soluții

Găsirea ODZ înseamnă găsirea tuturor valorilor valide care se potrivesc unei anumite funcții sau inegalități. Nerespectarea acestor condiții poate duce la rezultate incorecte. Pentru a găsi ODZ, este adesea necesar să treci prin transformări într-o anumită expresie.

Există expresii în care calculul lor este imposibil:

• dacă există împărțire la zero;
• luarea rădăcinii unui număr negativ;
• prezența unui indicator întreg negativ - numai pentru numere pozitive;
• calcularea logaritmului unui număr negativ;
• domeniul de definire a tangentei π 2 + π · k, k ∈ Z și cotangentei π · k, k ∈ Z;
• aflarea valorii arcsinusului și arccosinusului unui număr pentru o valoare care nu aparține lui [-1; 1].

Toate acestea arată cât de important este să ai ODZ.

Exemplul 3

Aflați expresia ODZ x 3 + 2 x y − 4 .

Soluţie

Orice număr poate fi cubit. Această expresie nu are o fracție, deci valorile lui x și y pot fi oricare. Adică ODZ este orice număr.

Răspuns: x și y – orice valoare.

Exemplul 4

Aflați ODZ al expresiei 1 3 - x + 1 0.

Soluţie

Se poate observa că există o fracție la care numitorul este zero. Aceasta înseamnă că pentru orice valoare a lui x vom obține împărțirea la zero. Aceasta înseamnă că putem concluziona că această expresie este considerată nedefinită, adică nu are nicio răspundere suplimentară.

Răspuns: ∅ .

Exemplul 5

Aflați ODZ a expresiei date x + 2 · y + 3 - 5 · x.

Soluţie

Prezența unei rădăcini pătrate înseamnă că această expresie trebuie să fie mai mare sau egală cu zero. Dacă este negativ, nu are sens. Aceasta înseamnă că este necesar să scrieți o inegalitate de forma x + 2 · y + 3 ≥ 0. Adică, acesta este intervalul dorit de valori acceptabile.

Răspuns: mulțime de x și y, unde x + 2 y + 3 ≥ 0.

Exemplul 6

Determinați expresia ODZ de forma 1 x + 1 - 1 + log x + 8 (x 2 + 3) .

Soluţie

Prin condiție, avem o fracție, deci numitorul ei nu ar trebui să fie egal cu zero. Obținem că x + 1 - 1 ≠ 0. Expresia radicală are întotdeauna sens atunci când este mai mare sau egală cu zero, adică x + 1 ≥ 0. Deoarece are un logaritm, expresia sa trebuie să fie strict pozitivă, adică x 2 + 3 > 0. Baza logaritmului trebuie să aibă și o valoare pozitivă și diferită de 1, apoi adăugăm condițiile x + 8 > 0 și x + 8 ≠ 1. Rezultă că ODZ dorit va lua forma:

x + 1 - 1 ≠ 0, x + 1 ≥ 0, x 2 + 3 > 0, x + 8 > 0, x + 8 ≠ 1

Cu alte cuvinte, se numește un sistem de inegalități cu o variabilă. Soluția va conduce la următoarea notație ODZ [ − 1, 0) ∪ (0, + ∞) .

Răspuns: [ − 1 , 0) ∪ (0 , + ∞)

De ce este important să luați în considerare DPD atunci când conduceți schimbarea?

În timpul transformărilor de identitate, este important să găsiți ODZ. Există cazuri în care nu apare existența ODZ. Pentru a înțelege dacă o expresie dată are o soluție, trebuie să comparați VA variabilelor expresiei inițiale și VA a celei rezultate.

Transformări de identitate:

• poate să nu afecteze DL;
• poate duce la extinderea sau adăugarea de DZ;
• poate îngusta DZ.

Să ne uităm la un exemplu.

Exemplul 7

Dacă avem o expresie de forma x 2 + x + 3 · x, atunci ODZ ei este definită pe întregul domeniu de definiție. Chiar și atunci când aducem termeni similari și simplificăm expresia, ODZ nu se schimbă.

Exemplul 8

Dacă luăm exemplul expresiei x + 3 x − 3 x, atunci lucrurile stau diferit. Avem o expresie fracțională. Și știm că împărțirea la zero este inacceptabilă. Atunci ODZ are forma (− ∞, 0) ∪ (0, + ∞) . Se vede că zero nu este o soluție, așa că îl adăugăm cu o paranteză.

Să luăm în considerare un exemplu cu prezența unei expresii radicale.

Exemplul 9

Dacă există x - 1 · x - 3, atunci ar trebui să acordați atenție ODZ, deoarece trebuie scrisă ca o inegalitate (x - 1) · (x - 3) ≥ 0. Este posibil să se rezolve prin metoda intervalului, atunci aflăm că ODZ va lua forma (− ∞, 1 ] ∪ [ 3 , + ∞) . După transformarea x - 1 · x - 3 și aplicarea proprietății rădăcinilor, avem că ODZ poate fi completat și totul poate fi scris sub forma unui sistem de inegalități de forma x - 1 ≥ 0, x - 3 ≥ 0. Când o rezolvăm, constatăm că [ 3 , + ∞) . Aceasta înseamnă că ODZ se scrie complet după cum urmează: (− ∞, 1 ] ∪ [ 3 , + ∞) .

Transformările care îngustează DZ trebuie evitate.

Exemplul 10

Să luăm în considerare un exemplu de expresie x - 1 · x - 3, când x = - 1. Când înlocuim, obținem că - 1 - 1 · - 1 - 3 = 8 = 2 2 . Dacă transformăm această expresie și o aducem la forma x - 1 · x - 3, atunci când calculăm constatăm că 2 - 1 · 2 - 3 expresia nu are sens, deoarece expresia radicală nu ar trebui să fie negativă.

Este necesar să se adere la transformări identice pe care ODZ nu se va schimba.

Dacă există exemple care se extind pe el, atunci ar trebui adăugat la DL.

Exemplul 11

Să ne uităm la exemplul unei fracții de forma x x 3 + x. Dacă anulăm cu x, atunci obținem acel 1 x 2 + 1. Apoi ODZ se extinde și devine (− ∞ 0) ∪ (0 , + ∞) . Mai mult, atunci când calculăm, lucrăm deja cu a doua fracție simplificată.

În prezența logaritmilor, situația este ușor diferită.

Exemplul 12

Dacă există o expresie de forma ln x + ln (x + 3), aceasta se înlocuiește cu ln (x · (x + 3)), pe baza proprietății logaritmului. Din aceasta putem vedea că ODZ de la (0 , + ∞) la (− ∞ , − 3) ∪ (0 , + ∞) . Prin urmare, pentru a determina ODZ ln (x · (x + 3)) este necesar să se efectueze calcule pe ODZ, adică mulțimea (0, + ∞).

La rezolvare, este întotdeauna necesar să se acorde atenție structurii și formei expresiei date. Dacă zona de definire este găsită corect, rezultatul va fi pozitiv.

Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Supraveghetor stiintific:

1. Introducere 3

2. Schiță istorică 4

3. „Locul” ODZ la rezolvarea ecuațiilor și inegalităților 5-6

4. Caracteristicile și pericolele ODZ 7

5. ODZ – există o soluție 8-9

6. Găsirea ODZ este o muncă suplimentară. Echivalența tranzițiilor 10-14

7. ODZ la Examenul Unificat de Stat 15-16

8. Concluzie 17

9. Literatură 18

1. Introducere

Problemă: ecuațiile și inegalitățile în care este necesar să se găsească ODZ nu și-au găsit loc în cursul de algebră pentru prezentarea sistematică, motiv pentru care, probabil, colegii mei și cu mine greșim adesea atunci când rezolvăm astfel de exemple, petrecând mult timp rezolvându-le, uitând în același timp. despre ODZ.

Ţintă: să poată analiza situația și să tragă concluzii logic corecte în exemple în care este necesar să se țină cont de DL.

Sarcini:

1. Material teoretic de studiu;

2. Rezolvați multe ecuații, inegalități: a) fracționar-rațional; b) irațional; c) logaritmică; d) conţinând funcţii trigonometrice inverse;

3. Aplica materialele studiate intr-o situatie diferita de cea standard;

4. Creați o lucrare pe tema „Zona valorilor acceptabile: teorie și practică”

Lucrați la proiect: Am început să lucrez la proiect repetând funcțiile pe care le cunoșteam. Sfera multora dintre ele este limitată.

ODZ apare:

1. La rezolvarea ecuațiilor raționale fracționale și a inegalităților

2. La rezolvarea ecuaţiilor şi inegalităţilor iraţionale

3. La rezolvarea ecuaţiilor logaritmice şi a inegalităţilor

4. La rezolvarea ecuaţiilor şi inegalităţilor care conţin funcţii trigonometrice inverse

După ce am rezolvat multe exemple din diverse surse (use manuale, manuale, cărți de referință), am sistematizat soluția exemplelor după următoarele principii:

· puteți rezolva exemplul și țineți cont de ODZ (cea mai comună metodă)

· este posibil să se rezolve exemplul fără a lua în considerare ODZ

· se poate ajunge la decizia corectă doar luând în considerare ODZ.

Metode utilizate în lucrare: 1) analiza; 2) analiza statistica; 3) deducere; 4) clasificare; 5) prognoza.

Am studiat analiza rezultatelor examenului unificat de stat în ultimii ani. S-au făcut multe greșeli în exemple în care este necesar să se țină cont de DL. Acest lucru subliniază încă o dată relevanţă subiectul meu.

2. Schiță istorică

Ca și alte concepte ale matematicii, conceptul de funcție nu s-a dezvoltat imediat, ci a trecut printr-o lungă cale de dezvoltare. În lucrarea lui P. Fermat „Introducerea și studiul locurilor plane și solide” (1636, publicată în 1679) se spune: „Ori de câte ori există două mărimi necunoscute în ecuația finală, există un loc”. În esență, aici vorbim despre dependența funcțională și reprezentarea ei grafică („loc” în Fermat înseamnă o linie). Studiul dreptelor după ecuațiile lor din „Geometria” (1637) a lui R. Descartes indică și o înțelegere clară a dependenței reciproce a două variabile. I. Barrow (Lectures on Geometry, 1670) stabilește sub formă geometrică natura inversă reciprocă a acțiunilor de diferențiere și integrare (desigur, fără a folosi acești termeni înșiși). Acest lucru indică deja o stăpânire complet clară a conceptului de funcție. Acest concept îl găsim și în formă geometrică și mecanică la I. Newton. Cu toate acestea, termenul „funcție” apare pentru prima dată abia în 1692 cu G. Leibniz și, în plus, nu chiar în înțelegerea sa modernă. G. Leibniz numește funcții diverse segmente asociate unei curbe (de exemplu, abscisa punctelor acesteia). În primul curs tipărit, „Analiza infinitezimale pentru cunoașterea liniilor curbe” de L'Hopital (1696), termenul de „funcție” nu este folosit.

Prima definiție a unei funcții într-un sens apropiat de cel modern se găsește în I. Bernoulli (1718): „O funcție este o mărime compusă dintr-o variabilă și o constantă”. Această definiție nu complet clară se bazează pe ideea de a specifica o funcție printr-o formulă analitică. Aceeași idee apare și în definiția lui L. Euler, dată de acesta în „Introduction to the Analysis of Infinites” (1748): „Funcția unei mărimi variabile este o expresie analitică compusă într-un fel din această mărime variabilă și numere sau cantități constante.” Cu toate acestea, L. Euler nu mai este străin de înțelegerea modernă a funcției, care nu leagă conceptul de funcție cu niciuna dintre expresiile sale analitice. „Calcul diferențial” al său (1755) spune: „Când anumite cantități depind de altele în așa fel încât atunci când acestea din urmă se schimbă, ele însele sunt supuse modificării, atunci primele sunt numite funcții ale celei din urmă.”

De la începutul secolului al XIX-lea, conceptul de funcție a fost din ce în ce mai definit fără a menționa reprezentarea sa analitică. În „Tratat de calcul diferențial și integral” (1797-1802) S. Lacroix spune: „Orice mărime a cărei valoare depinde de una sau mai multe alte mărimi se numește o funcție a acestora din urmă”. În „Teoria analitică a căldurii” de J. Fourier (1822) există o frază: „Funcție f(x) denotă o funcție complet arbitrară, adică o succesiune de valori date, supuse sau nu unei legi generale și corespunzătoare tuturor valorilor x cuprinsă între 0 și o anumită valoare x" Definiția lui N. I. Lobachevsky este apropiată de cea modernă: „...Conceptul general de funcție cere ca o funcție din x numiți numărul care este dat pentru fiecare x si impreuna cu x se schimba treptat. Valoarea unei funcții poate fi dată fie printr-o expresie analitică, fie printr-o condiție care oferă un mijloc de testare a tuturor numerelor și de a alege unul dintre ele sau, în sfârșit, dependența poate exista și rămâne necunoscută. Se mai spune ceva mai jos: „Viziunea largă a teoriei permite existența dependenței doar în sensul că numerele unul cu altul în legătură sunt înțelese ca și cum ar fi date împreună.” Astfel, definiția modernă a unei funcții, lipsită de referințe la sarcina analitică, atribuită de obicei lui P. Dirichlet (1837), a fost propusă în repetate rânduri înaintea acestuia.

Domeniul de definire (valori admisibile) al unei funcții y este mulțimea de valori ale variabilei independente x pentru care este definită această funcție, adică domeniul de modificare a variabilei independente (argument).

3. „Locul” intervalului de valori acceptabile atunci când se rezolvă ecuații și inegalități

1. La rezolvarea ecuațiilor raționale fracționale și a inegalităților numitorul nu trebuie să fie zero.

2. Rezolvarea ecuațiilor și inegalităților iraționale.

2.1..gif" width="212" height="51"> .

În acest caz, nu este nevoie să găsiți ODZ: din prima ecuație rezultă că valorile obținute ale lui x satisfac următoarea inegalitate: https://pandia.ru/text/78/083/images/image004_33. gif" width="107" height="27 src="> este sistemul:

Deoarece intră în ecuație în mod egal, atunci, în loc de inegalitate, puteți include inegalitatea https://pandia.ru/text/78/083/images/image009_18.gif" width="220" height="49">

https://pandia.ru/text/78/083/images/image014_11.gif" width="239" height="51">

3. Rezolvarea ecuațiilor logaritmice și a inegalităților.

3.1. Schema de rezolvare a unei ecuații logaritmice

Dar este suficient să verificați o singură condiție a ODZ.

3.2..gif" width="115" height="48 src=">.gif" width="115" height="48 src=">

4. Ecuații trigonometrice de formă sunt echivalente cu sistemul (în loc de inegalitate, puteți include inegalitatea în sistem https://pandia.ru/text/78/083/images/image024_5.gif" width="377" height="23"> sunt echivalente la ecuație

4. Caracteristici și pericole ale gamei de valori admisibile

La lecțiile de matematică, ni se cere să găsim DL în fiecare exemplu. În același timp, conform esenței matematice a problemei, găsirea ODZ nu este deloc obligatorie, adesea nu este necesară și, uneori, imposibilă - și toate acestea fără nicio deteriorare a soluției exemplului. Pe de altă parte, se întâmplă adesea ca, după rezolvarea unui exemplu, școlarii să uite să țină cont de DL, să îl noteze ca răspuns final și să țină cont doar de anumite condiții. Această împrejurare este binecunoscută, dar „războiul” continuă în fiecare an și, se pare, va continua mult timp.

Luați în considerare, de exemplu, următoarea inegalitate:

Aici se caută ODZ și se rezolvă inegalitatea. Cu toate acestea, atunci când rezolvă această inegalitate, școlarii cred uneori că este foarte posibil să se facă fără a căuta DL sau, mai precis, este posibil să se facă fără condiție

De fapt, pentru a obține răspunsul corect este necesar să se țină cont atât de inegalitatea , cât și de .

Dar, de exemplu, soluția ecuației: https://pandia.ru/text/78/083/images/image032_4.gif" width="79 height=75" height="75">

ceea ce este echivalent cu lucrul cu ODZ. Cu toate acestea, în acest exemplu, o astfel de muncă este inutilă - este suficient să verificați îndeplinirea a doar două dintre aceste inegalități și oricare două.

Permiteți-mi să vă reamintesc că orice ecuație (inegalitate) poate fi redusă la forma . ODZ este pur și simplu domeniul de definire al funcției din partea stângă. Faptul că această zonă trebuie monitorizată rezultă din definirea rădăcinii ca număr din domeniul de definire a unei anumite funcții, deci din ODZ. Iată un exemplu amuzant pe acest subiect..gif" width="20" height="21 src="> are un domeniu de definire a unui set de numere pozitive (acesta, desigur, este un acord pentru a lua în considerare o funcție cu , dar rezonabil), și atunci -1 nu este este rădăcina.

5. Gama de valori acceptabile – există o soluție

Și, în sfârșit, într-o mulțime de exemple, găsirea ODZ vă permite să obțineți răspunsul fără machete voluminoase, sau chiar verbal.

1. OD3 este un set gol, ceea ce înseamnă că exemplul original nu are soluții.

1) 2) 3)

2. B ODZ se găsesc unul sau mai multe numere, iar o simplă înlocuire determină rapid rădăcinile.

1) , x=3

2)Aici în ODZ există doar numărul 1, iar după înlocuire este clar că nu este o rădăcină.

3) Există două numere în ODZ: 2 și 3 și ambele sunt potrivite.

4) > În ODZ există două numere 0 și 1, și numai 1 este potrivit.

ODZ poate fi utilizat eficient în combinație cu analiza expresiei în sine.

5) < ОДЗ: Но в правой части неравенства могут быть только положительные числа, поэтому оставляем х=2. Тогда в неравенство подставим 2.

6) Din ODZ rezultă că, unde avem ..gif" width="143" height="24"> Din ODZ avem: . Dar apoi și . Deoarece, nu există soluții.

Din ODZ avem: https://pandia.ru/text/78/083/images/image060_0.gif" width="48" height="24">>, ceea ce înseamnă . Rezolvând ultima inegalitate, obținem x<- 4, что не входит в ОДЗ. По­этому решения нет.

3) ODZ: . De atunci

Pe de altă parte, https://pandia.ru/text/78/083/images/image068_0.gif" width="160" height="24">

ODZ:. Se consideră ecuația pe intervalul [-1; 0).

Îndeplinește următoarele inegalități https://pandia.ru/text/78/083/images/image071_0.gif" width="68" height="24 src=">.gif" width="123" height="24 src="> și nu există soluții. Cu funcția și https://pandia.ru/text/78/083/images/image076_0.gif" width="179" height="25">. ODZ: x>2..gif" width="233" height ="45 src="> Să găsim ODZ:

O soluție întreagă este posibilă numai pentru x=3 și x=5. Prin verificare constatăm că rădăcina x=3 nu se potrivește, ceea ce înseamnă că răspunsul este x=5.

6. Găsirea intervalului de valori acceptabile este o muncă suplimentară. Echivalența tranzițiilor.

Puteți da exemple în care situația este clară chiar și fără a găsi DZ.

1.

Egalitatea este imposibilă, deoarece la scăderea unei expresii mai mari dintr-o expresie mai mică, rezultatul trebuie să fie un număr negativ.

2. .

Suma a două funcții nenegative nu poate fi negativă.

De asemenea, voi da exemple în care găsirea ODZ este dificilă și uneori pur și simplu imposibilă.

Și, în cele din urmă, căutările pentru ODZ sunt foarte adesea doar o muncă suplimentară, de care te poți descurca, dovedind astfel înțelegerea a ceea ce se întâmplă. Există un număr mare de exemple care pot fi date aici, așa că le voi alege doar pe cele mai tipice. Principala metodă de soluție în acest caz este transformările echivalente la trecerea de la o ecuație (inegalitate, sistem) la alta.

1.. ODZ nu este necesar, deoarece, după ce am găsit acele valori ale lui x pentru care x2 = 1, nu putem obține x = 0.

2. . ODZ nu este necesar, deoarece aflăm când expresia radicală este egală cu un număr pozitiv.

3. . ODZ nu este necesar din aceleași motive ca în exemplul anterior.

4.

ODZ nu este necesar, deoarece expresia radicală este egală cu pătratul unei anumite funcții și, prin urmare, nu poate fi negativă.

5.

6. ..gif" width="271" height="51"> Pentru a rezolva este suficientă o singură restricție pentru expresia radicală.De fapt, din sistemul mixt scris rezultă că cealaltă expresie radicală este nenegativă.

8. DZ nu este necesar din aceleași motive ca în exemplul anterior.

9. ODZ nu este necesar, deoarece este suficient ca două dintre cele trei expresii de sub semnele logaritmului să fie pozitive pentru a asigura pozitivitatea celei de-a treia.

10. .gif" width="357" height="51"> ODZ nu este necesar din aceleași motive ca în exemplul anterior.

Este de remarcat, totuși, că atunci când se rezolvă folosind metoda transformărilor echivalente, cunoașterea ODZ (și proprietățile funcțiilor) ajută.

Iată câteva exemple.

1. . OD3, ceea ce presupune că expresia din partea dreaptă este pozitivă și este posibil să scrieți o ecuație echivalentă cu aceasta în această formă https://pandia.ru/text/78/083/images/image101_0.gif" width ="112" height="27 "> ODZ: Dar atunci, și la rezolvarea acestei inegalități, nu este necesar să luăm în considerare cazul când partea dreaptă este mai mică de 0.

3. . Din ODZ rezultă că și, prin urmare, este cazul când https://pandia.ru/text/78/083/images/image106_0.gif" width="303" height="48"> Tranziția în general arată astfel :

https://pandia.ru/text/78/083/images/image108_0.gif" width="303" height="24">

Există două cazuri posibile: 0 >1.

Aceasta înseamnă că inegalitatea inițială este echivalentă cu următorul set de sisteme de inegalități:

Primul sistem nu are soluții, dar din al doilea obținem: x<-1 – решение неравенства.

Înțelegerea condițiilor de echivalență necesită cunoașterea unor subtilități. De exemplu, de ce sunt echivalente următoarele ecuații:

Sau

Și în sfârșit, poate cel mai important. Cert este că echivalența garantează corectitudinea răspunsului dacă se fac unele transformări ale ecuației în sine, dar nu este folosită pentru transformări doar în una dintre părți. Abrevierile și utilizarea diferitelor formule într-una dintre părți nu sunt acoperite de teoremele de echivalență. Am dat deja câteva exemple de acest tip. Să ne uităm la câteva exemple.

1. Această decizie este firească. În partea stângă, conform proprietății funcției logaritmice, trecem la expresia ..gif" width="111" height="48">

După ce am rezolvat acest sistem, obținem rezultatul (-2 și 2), care, totuși, nu este un răspuns, deoarece numărul -2 nu este inclus în ODZ. Deci, trebuie să stabilim ODS? Desigur că nu. Dar din moment ce am folosit o anumită proprietate a funcției logaritmice în soluție, atunci suntem obligați să furnizăm condițiile în care aceasta este satisfăcută. O astfel de condiție este pozitivitatea expresiilor sub semnul logaritmului..gif" width="65" height="48">.

2. ..gif" width="143" height="27 src="> numerele pot fi înlocuite în acest fel . Cine vrea să facă astfel de calcule plictisitoare?.gif" width="12" height="23 src="> adăugați o condiție și puteți vedea imediat că doar numărul https://pandia.ru/text/78/083 / îndeplinește această condiție images/image128_0.gif" width="117" height="27 src=">) a fost demonstrat de 52% dintre participanții la testare. Unul dintre motivele pentru rate atât de scăzute este faptul că mulți absolvenți nu au selectat rădăcinile obținute din ecuație după pătrat-o.

3) Luați în considerare, de exemplu, soluția uneia dintre problemele C1: „Găsiți toate valorile lui x pentru care punctele graficului funcției se află deasupra punctelor corespunzătoare ale graficului funcției ". Sarcina se rezumă la rezolvarea unei inegalități fracționale care conține o expresie logaritmică. Cunoaștem metodele de rezolvare a unor astfel de inegalități. Cea mai comună dintre ele este metoda intervalelor. Cu toate acestea, când folosindu-l, cei care iau testul fac diverse greșeli Să luăm în considerare cele mai frecvente erori folosind exemplul inegalității:

X< 10. Они отмечают, что в первом случае решений нет, а во втором – корнями являются числа –1 и . При этом выпускники не учитывают условие x < 10.

8. Concluzie

Pentru a rezuma, putem spune că nu există o metodă universală de rezolvare a ecuațiilor și inegalităților. De fiecare dată, dacă vrei să înțelegi ce faci și să nu acționezi mecanic, apare o dilemă: ce soluție ar trebui să alegi, în special, să cauți sau nu ODZ? Cred că experiența pe care am acumulat-o mă va ajuta să rezolv această dilemă. Voi înceta să mai greșesc învățând cum să folosesc corect ODZ. Dacă pot face asta, timpul sau, mai degrabă, examenul unificat de stat, va spune.

9. Literatură

Și alții „Algebra și începuturile analizei 10-11” carte de probleme și manual, M.: „Prosveshchenie”, 2002. „Manual de matematică elementară”. M.: „Nauka”, 1966. Ziarul „Matematica” Nr. 46, Ziarul „Matematica” Nr. Ziarul „Matematica” Nr. „Istoria matematicii în clasele VII-VIII”. M.: „Prosveshcheniye”, 1982. etc. „Cea mai completă ediție a versiunilor sarcinilor reale de examinare unificată de stat: 2009/FIPI” - M.: „Astrel”, 2009. etc. „Examinare unificată de stat. Matematică. Materiale universale pentru pregătirea elevilor/FIPI” - M.: „Centrul de Informaţii”, 2009. etc. „Algebra şi începuturile analizei 10-11”. M.: „Prosveshchenie”, 2007. „Atelier de rezolvare a problemelor la matematica școlară (atelier de algebră).” M.: Educație, 1976. „25.000 de lecții de matematică”. M.: „Iluminismul”, 1993. „Pregătirea pentru olimpiadele de matematică”. M.: „Examen”, 2006. „Enciclopedie pentru copii „MATEMATICĂ”” volumul 11, M.: Avanta +; 2002. Materiale de pe site-urile www. *****, www. *****.

În matematică există un număr destul de mic de funcții elementare, al căror domeniu de aplicare este limitat. Toate celelalte funcții „complexe” sunt doar combinații și combinații ale acestora.

1. Funcție fracțională - restricție asupra numitorului.

2. Rădăcină de grad par - restricție asupra expresiei radicale.

3. Logaritmi - restricții pe baza logaritmului și a expresiei sublogaritmice.

3. Trigonometric tg(x) și ctg(x) - restricție asupra argumentului.

Pentru tangentă:

4. Funcții trigonometrice inverse.

arcsinus	arc cosinus	Arctangent, Arctangent

În continuare, următoarele exemple sunt rezolvate pe tema „Domeniul de definire a funcțiilor”.

Exemplul 1

Exemplul 2

Exemplul 3

Exemplul 4

Exemplul 5

Exemplul 6

Exemplul 7

Exemplul 8

Exemplul 9

Exemplul 10

Exemplul 11

Exemplul 12

Exemplul 13

Exemplul 14

Exemplul 15

Exemplul 16

Un exemplu de găsire a domeniului de definire a funcției nr. 1

Găsirea domeniului de definire al oricărei funcții liniare, i.e. functii de gradul I:

y = 2x + 3 - ecuația definește o dreaptă pe un plan.

Să ne uităm cu atenție la funcție și să ne gândim la ce valori numerice putem înlocui în ecuație în loc de variabila x?

Să încercăm să înlocuim valoarea x=0

Deoarece y = 2 0 + 3 = 3 - a primit o valoare numerică, prin urmare funcția există pentru valoarea dată a variabilei x=0.

Să încercăm să înlocuim valoarea x=10

întrucât y = 2·10 + 3 = 23 - funcția există pentru valoarea dată a variabilei x = 10.

Să încercăm să înlocuim valoarea x=-10

întrucât y = 2·(-10) + 3 = -17 - funcția există pentru valoarea dată a variabilei x = -10.

Ecuația definește o linie dreaptă pe un plan, iar o linie dreaptă nu are nici început, nici sfârșit, de aceea există pentru orice valoare a lui x.

Rețineți că indiferent de ce valori numerice înlocuim într-o funcție dată în loc de x, vom obține întotdeauna valoarea numerică a variabilei y.

Prin urmare, funcția există pentru orice valoare x ∈ R, sau o scriem astfel: D(f) = R

Forme de scriere a răspunsului: D(f)=R sau D(f)=(-∞:+∞)sau x∈R sau x∈(-∞:+∞)

Să conchidem:

Pentru orice funcție de forma y = ax + b, domeniul de definiție este mulțimea numerelor reale.

Un exemplu de găsire a domeniului de definire a funcției nr. 2

O functie de forma:

y = 10/(x + 5) - ecuația hiperbolei

Când aveți de-a face cu o funcție fracțională, amintiți-vă că nu puteți împărți la zero. Prin urmare, funcția va exista pentru toate valorile lui x care nu sunt

setați numitorul la zero. Să încercăm să înlocuim câteva valori arbitrare pentru x.

La x = 0 avem y = 10/(0 + 5) = 2 - funcția există.

Pentru x = 10 avem y = 10/(10 + 5) = 10/15 = 2/3- funcția există.

La x = -5 avem y = 10/(-5 + 5) = 10/0 - funcția nu există în acest moment.

Aceste. dacă funcția dată este fracțională, atunci este necesar să echivalăm numitorul cu zero și să găsim un punct în care funcția nu există.

In cazul nostru:

x + 5 = 0 → x = -5 - în acest moment funcția dată nu există.

x + 5 ≠ 0 → x ≠ -5

Pentru claritate, să-l descriem grafic:

Pe grafic vedem, de asemenea, că hiperbola se apropie cât mai mult de dreapta x = -5, dar nu atinge însăși valoarea -5.

Vedem că funcția dată există în toate punctele axei reale, cu excepția punctului x = -5

Formulare de înregistrare a răspunsurilor: D(f)=R\(-5) sau D(f)=(-∞;-5) ∪ (-5;+∞) sau x ∈ R\(-5) sau x ∈ (-∞;-5) ∪ (-5;+∞)

Dacă funcția dată este fracțională, atunci prezența unui numitor impune condiția ca numitorul să nu fie egal cu zero.

Un exemplu de găsire a domeniului de definire a funcției nr. 3

Să luăm în considerare un exemplu de găsire a domeniului de definire al unei funcții cu rădăcină de grad par:

Deoarece putem extrage doar rădăcina pătrată dintr-un număr nenegativ, prin urmare, funcția de sub rădăcină este nenegativă.

2x - 8 ≥ 0

Să rezolvăm o inegalitate simplă:

2x - 8 ≥ 0 → 2x ≥ 8 → x ≥ 4

Funcția specificată există numai pentru valorile găsite ale lui x ≥ 4 sau D(f)=)